题目内容
14.给出下列四个结论:①如果$\overrightarrow a•\overrightarrow b=\overrightarrow a•\overrightarrow c,且\overrightarrow a≠\overrightarrow 0$,那么$\overrightarrow b,\overrightarrow c$在$\overrightarrow a$方向上的投影相等
②已知平面α和互不相同的三条直线m、n、l,若l、m是异面直线,m∥α,l∥α、且n⊥l,n⊥m,则n⊥α;
③过平面α的一条斜线有一个平面与平面α垂直
④设回归直线方程为$\hat y=2-2.5x$,当变量x增加一个单位时,$\hat y$平均增加2个单位
其中正确结论的个数为 ( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 ①根据向量的数量积以及向量投影的定义进行判断.
②根据线面垂直的判定定理以及异面直线的性质进行判断.
③根据面面垂直的判定定理进行判断.
④根据线性回归直线方程的性质进行判断.
解答 解:①如果$\overrightarrow a•\overrightarrow b=\overrightarrow a•\overrightarrow c,且\overrightarrow a≠\overrightarrow 0$,
则|$\overrightarrow a$||$\overrightarrow{b}$|cos<$\overrightarrow a$,$\overrightarrow{b}$>=|$\overrightarrow a$||$\overrightarrow{c}$|cos<$\overrightarrow a$,$\overrightarrow{c}$>,
即|$\overrightarrow{b}$|cos<$\overrightarrow a$,$\overrightarrow{b}$>=|$\overrightarrow{c}$|cos<$\overrightarrow a$,$\overrightarrow{c}$>,
那么$\overrightarrow b,\overrightarrow c$在$\overrightarrow a$方向上的投影相等,故①正确,
②∵l、m是异面直线,l∥α,m∥α,且n⊥l,n⊥m,∴l、m在平面α内的射影是两条相交直线,
且n垂直于平面α内的这两条射影,故n⊥α成立,故②正确.
③可过斜线与平面α的交点作一条垂直于平面α的直线,则斜线与垂线所确定的平面即与平面α垂直,这样的平面有且只有一个.故③正确.
④设回归直线方程为$\hat y=2-2.5x$,当变量x增加一个单位时,$\hat y$平均减少2.5个单位,故④错误,
故正确是①②③,
故选:C
点评 本题主要考查命题的真假判断,涉及的知识点较多,综合性较强,有一定的难度.

 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案| 车流量(万辆) | 0~10 | 11~50 | 51~70 | 71~80 | 81~100 | >100 |
| 拥挤等级 | 优 | 良 | 轻度拥挤 | 中度拥挤 | 重度拥挤 | 严重拥挤 |
| 日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 107日 |
| 车流量(万辆) | 120 | 110 | 85 | 75 | 60 | 105 | 110 |
(2)某人国庆节连续2天到该城市游玩,求这2天他遇到的车流量拥挤等级均为严重拥挤的概率.
| 调查人群态度 | 赞成 | 反对 | 无所谓 |
| 农村居民 | 2100人 | 120人 | y人 |
| 城镇居民 | 600人 | x人 | z人 |
(1)现用分层抽样的方法在所有参与调查的人中抽取360人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
(2)在持“反对”态度的人中,用分层抽样的方法抽取6人,抽到农村居民和城镇居民各多少人?在抽取的6人中选取2人进行深入交流,求至少有1人为城镇居民的概率.
| A. | 等差数列 | B. | 等比数列 | ||
| C. | 从第二项起为等差数列 | D. | 从第二项起为等比数列 |
| A. | (-3,0) | B. | (-$\frac{1}{3}$,1) | C. | (0,2) | D. | (-$\frac{1}{3}$,log32) |

| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
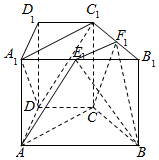 如图,在棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD为直角梯形,其中AB∥CD,AB⊥AD,AB=AC=2CD=2,AA1=$\sqrt{3}$,过AC的平面分别与A1B1,B1C1交于E1,F1,且E1为A1B1的中点.
如图,在棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD为直角梯形,其中AB∥CD,AB⊥AD,AB=AC=2CD=2,AA1=$\sqrt{3}$,过AC的平面分别与A1B1,B1C1交于E1,F1,且E1为A1B1的中点. 长时间用手机上网严重影响着学生的身体健康,某校为了解A、B两班学生手机上网的时长,分别从这两个班中随机抽取5名同学进行调查,将他们平均每周手机上网的时长作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).
长时间用手机上网严重影响着学生的身体健康,某校为了解A、B两班学生手机上网的时长,分别从这两个班中随机抽取5名同学进行调查,将他们平均每周手机上网的时长作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).