题目内容
7.已知函数$f(x)=\left\{{\begin{array}{l}{3+{{log}_2}x,x>0}\\{2{x^2}-3x,x≤0}\end{array}}\right.$,则不等式f(x)≤5的解集为( )| A. | [-1,1] | B. | (-∞,-1]∪(0,1) | C. | [-1,4] | D. | (-∞,-1]∪[0,4] |
分析 根据分段函数的表达式,对x进行分类讨论进行求解即可.
解答 解:若x>0,由f(x)≤5得3+log2x≤5,即log2x≤2,即0<x≤4,此时0<x≤4,
若x≤0,则由f(x)≤5得2x2-3x≤5即2x2-3x-5≤0,得-1≤x≤$\frac{5}{2}$,此时-1≤x≤0
综上-1≤x≤4,
即不等式的解集为[-1,4],
故选:C
点评 本题主要考查不等式的求解,根据分段函数的表达式,对x进行分类讨论是解决本题的关键.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
19.数列{an}中,已知a1=1,S2=2,且Sn+1+2Sn-1=3Sn(n≥2,n∈N*),则数列{an}为( )
| A. | 等差数列 | B. | 等比数列 | ||
| C. | 从第二项起为等差数列 | D. | 从第二项起为等比数列 |
17.某单位共有职工150名,其中高级职称45人,中级职称90人,初级职称15人.现采用分层抽样方法从中抽取容量为30的样本,则各职称人数分别为( )
| A. | 9,18,3 | B. | 10,15,5 | C. | 10,17,3 | D. | 9,16,5 |
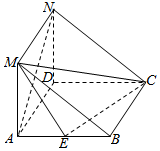 如图,在三棱柱ABM-DCN中,侧面ADNM⊥侧面ABCD,且侧面ABCD是菱形,∠DAB=60°,AD=2,侧面ADNM是矩形,AM=1.E是AB的中点.
如图,在三棱柱ABM-DCN中,侧面ADNM⊥侧面ABCD,且侧面ABCD是菱形,∠DAB=60°,AD=2,侧面ADNM是矩形,AM=1.E是AB的中点. 长时间用手机上网严重影响着学生的身体健康,某校为了解A、B两班学生手机上网的时长,分别从这两个班中随机抽取5名同学进行调查,将他们平均每周手机上网的时长作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).
长时间用手机上网严重影响着学生的身体健康,某校为了解A、B两班学生手机上网的时长,分别从这两个班中随机抽取5名同学进行调查,将他们平均每周手机上网的时长作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).