题目内容
1. 设P、Q是单位正方体AC1的面AA1D1D、面A1B1C1D1的中心.
设P、Q是单位正方体AC1的面AA1D1D、面A1B1C1D1的中心.(1)求∠D1B1C的大小.
(2)证明:PQ∥平面AA1B1B.
(3)求异面直线PQ和B1C所成的角.
分析 (1)连接CD1,由等边三角形得出∠D1B1C的大小;
(2)连接AD1,AB1,证明PQ∥AB1即可;
(3)连接AC,找出异面直线PQ和B1C所成的角,求出即可.
解答  解:(1)如图所示;
解:(1)如图所示;
连接CD1,则△D1B1C是等边三角形,
∴∠D1B1C=60°;
(2)证明:连接AD1,AB1,则P、Q分别AD1、B1D1的中点,
∴PQ∥AB1,
又PQ?平面AA1B1B,AB1?平面AA1B1B,
∴PQ∥平面AA1B1B;
(3)连接AC,∵PQ∥AB1,
∠AB1C为异面直线PQ和B1C所成的角或补角,
∵△AB1C为等边三角形,∴∠AB1C=60°,
∴异面直线PQ和B1C所成的角为60°.
点评 本题考查了空间中的线线平行与线面平行问题,也考查了空间角的定义与计算问题,是综合性题目.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
7.对空间任一点O和不共线三点A,B,C,能得到P,A,B,C四点共面的是( )
| A. | $\overrightarrow{OP}$=$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$ | B. | $\overrightarrow{OP}$=$\frac{1}{3}$$\overrightarrow{OA}$+$\frac{1}{3}$$\overrightarrow{OB}$+$\frac{1}{3}$$\overrightarrow{OC}$ | ||
| C. | $\overrightarrow{OP}$=-$\overrightarrow{OA}$+$\frac{1}{2}$$\overrightarrow{OB}$+$\frac{1}{2}$$\overrightarrow{OC}$ | D. | 以上皆错 |
6.如图,在四形边ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°.将△ADB沿BD折起,使CD⊥平面ABD,构成三棱锥A-BCD.则在三棱锥A-BCD中,下列结论正确的是( )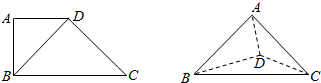

| A. | AD⊥平面BCD | B. | AB⊥平面BCD | C. | 平面BCD⊥平面ABC | D. | 平面ADC⊥平面ABC |
10.函数$f(x)=\frac{{\sqrt{x+2}}}{x-1}$的定义域为( )
| A. | {x|x≥-2且x≠1} | B. | {x|x≥-2} | C. | {x|x≥-2或x≠1} | D. | {x|x≠1} |
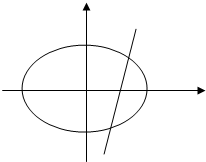 已知椭圆:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左右焦点分别为F1(-1,0),F2(1,0),且过点$(-1,\frac{3}{2})$,右顶点为A,经过点F2的动直线l与椭圆交于B,C两点.
已知椭圆:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左右焦点分别为F1(-1,0),F2(1,0),且过点$(-1,\frac{3}{2})$,右顶点为A,经过点F2的动直线l与椭圆交于B,C两点.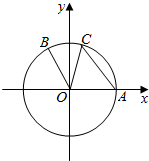 如图,在平面直角坐标系xOy中,以原点为圆心的圆O与x轴的正半轴交于点A,点B(-1,2)在圆O上,点C在弧AB上,且∠BOC为$\frac{π}{4}$.
如图,在平面直角坐标系xOy中,以原点为圆心的圆O与x轴的正半轴交于点A,点B(-1,2)在圆O上,点C在弧AB上,且∠BOC为$\frac{π}{4}$.