题目内容
12.椭圆的中心为坐标原点,长、短轴长之比为$\frac{2}{1}$,一个焦点是(0,-2),试求椭圆的离心率和椭圆的标准方程.分析 根据题意,由椭圆的焦点坐标可得a2-b2=4①,又由其长、短轴长之比为$\frac{2}{1}$,可得$\frac{2a}{2b}$=$\frac{2}{1}$②,联立①②,解可得a2、b2的值,由椭圆的离心率公式计算椭圆的离心率,将a2、b2的值代入椭圆的方程即可得椭圆的标准方程.
解答 解:根据题意,椭圆的一个焦点是(0,-2),即c=2,则有a2-b2=4,①
又由其长、短轴长之比为$\frac{2}{1}$,即$\frac{2a}{2b}$=$\frac{2}{1}$,②
联立①②,解可得a2=$\frac{16}{3}$,b2=$\frac{4}{3}$,
即a=$\frac{4\sqrt{3}}{3}$,其离心率e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$,
其标准方程为:$\frac{{y}^{2}}{\frac{16}{3}}$+$\frac{{x}^{2}}{\frac{4}{3}}$=1.
点评 本题考查椭圆的几何性质,关键是求出椭圆的标准方程,注意椭圆的焦点在y轴上.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
3.数列{an}中,a1=1,an+1=2an+2,则a7的值为( )
| A. | 94 | B. | 96 | C. | 190 | D. | 192 |
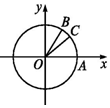 在如图所示的直角坐标系xOy中,点A,B是单位圆上的点,且A(1,0),∠AOB=$\frac{π}{3}$.现有一动点C在单位圆的劣弧$\widehat{AB}$上运动,设∠AOC=α.
在如图所示的直角坐标系xOy中,点A,B是单位圆上的点,且A(1,0),∠AOB=$\frac{π}{3}$.现有一动点C在单位圆的劣弧$\widehat{AB}$上运动,设∠AOC=α.