题目内容
7.已知圆C过两点M(-3,3),N(1,-5),且圆心C在直线2x-y-2=0上.(Ⅰ)求圆C的标准方程;
(Ⅱ)直线l过点(-2,5)且与圆C有两个不同的交点A,B,若直线l的斜率k大于0,求k的取值范围;
(Ⅲ)在(Ⅱ)的条件下,是否存在直线l使得弦AB的垂直平分线过点P(3,-1),若存在,求出直线l的方程;若不存在,请说明理由.
分析 (Ⅰ)由M(-3,3),N(1,-5),得MN的垂直平分线方程,和已知直线联立解得圆心坐标,再由R2=|CM|2求出半径,则圆C的标准方程可求;
(Ⅱ)设直线l的方程为:y-5=k(x+2)即kx-y+2k+5=0,设C到直线l的距离为d,由点到直线的距离公式结合题意求得k的取值范围;
(Ⅲ)设符合条件的直线l存在,则AB的垂直平分线方程为:y+1=-$\frac{1}{k}$(x-3)即:x+ky+k-3=0,由弦的垂直平分线过圆心(1,0)得k的值,即可求出符合条件的直线的方程.
解答 解:(Ⅰ)由M(-3,3),N(1,-5),得MN的垂直平分线方程为:x-2y-1=0,
联立$\left\{\begin{array}{l}{x-2y-1=0}\\{2x-y-2=0}\end{array}\right.$,解得圆心坐标为C(1,0),
R2=|CM|2=(-3-1)2+(3-0)2=25.
∴圆C的标准方程为:(x-1)2+y2=25;
(Ⅱ)设直线l的方程为:y-5=k(x+2)即kx-y+2k+5=0,设C到直线l的距离为d,
则d=$\frac{|3k+5|}{\sqrt{{k}^{2}+1}}$,
由题意:d<5 即:8k2-15k>0,
∴k<0或k>$\frac{15}{8}$,
又∵k>0,
∴k的取值范围是($\frac{15}{8}$,+∞);
(III)设符合条件的直线l存在,则AB的垂直平分线方程为:y+1=-$\frac{1}{k}$(x-3)即:x+ky+k-3=0,
∵弦的垂直平分线过圆心(1,0),∴k-2=0,即k=2.
∵k=2>$\frac{15}{8}$,
故符合条件的直线存在,l的方程为:x+2y-1=0.
点评 本题考查了圆的标准方程,考查了点到直线的距离公式的应用,是中档题.

| A. |  | B. |  | C. |  | D. |  |
| A. | 恒为负值 | B. | 恒为正值 | C. | 恒为零 | D. | 无法确定正负 |
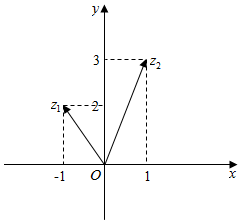 如图,已知向量$\overrightarrow{O{Z}_{1}}$与$\overrightarrow{O{Z}_{2}}$对应的复数是z1与z2
如图,已知向量$\overrightarrow{O{Z}_{1}}$与$\overrightarrow{O{Z}_{2}}$对应的复数是z1与z2