题目内容
（sin
+cos
）2的值为（ ）
| π |
| 8 |
| π |
| 8 |
A、1-
| ||||
B、1+
| ||||
C、
| ||||
D、1+
|
考点：二倍角的正弦,同角三角函数间的基本关系
专题：三角函数的求值
分析：根据三角函数的公式进行化简即可得到结论．
解答：
解：（sin
+cos
）2=sin2
+cos2
+2sin
cos
=1+sin
=1+
，
故选：B
| π |
| 8 |
| π |
| 8 |
| π |
| 8 |
| π |
| 8 |
| π |
| 8 |
| π |
| 8 |
| π |
| 4 |
| ||
| 2 |
故选：B
点评：本题主要考查函数值的计算，利用二倍角的正弦公式是解决本题的关键．
练习册系列答案
全优考典单元检测卷及归类总复习系列答案
品学双优卷系列答案
相关题目
下列函数中，最小值为4的是（ ）
A、y=x+
| ||
B、y=sinx+
| ||
| C、y=3x+4•3-x | ||
| D、y=log3x+4logx3 |
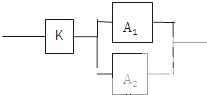如图．用K，A1，A2分别不同的原件连接成一个系统．当K正常工作且A1和A2正常工作的概率是0.9，0.8，0.8则系统正常工作的概率为（ ）| A、0.960 | B、0.864 |
| C、0.72 | D、0.576 |
若f′（x0）=-3，则
=（ ）
| lim |
| h→0 |
| f(x0+h)-f(x0-3h) |
| h |
| A、-3 | B、-12 | C、-9 | D、-6 |
已知向量
=（-
，
），且向量
在向量
的方向上的投影为
，则
•
为（ ）
| a |
| 12 |
| 13 |
| 5 |
| 13 |
| b |
| a |
| 13 |
| a |
| b |
A、
| ||
B、
| ||
| C、13 | ||
D、
|
定义在（0，+∞）上的可导函数f（x）满足：xf′（x）+f（x）＜0且f（1）=1，则不等式xf（x）＞1的解集为（ ）
| A、（-∞，1） |
| B、（0，1） |
| C、（1，+∞） |
| D、（0，1] |