题目内容
10.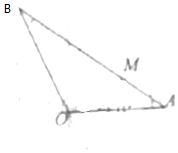 如图,在△AOB中,∠AOB=$\frac{3π}{4}$,OA=6,M为边AB上一点,M到边OA,OB的距离分别为2,2$\sqrt{2}$,则AB的长为6$\sqrt{5}$.
如图,在△AOB中,∠AOB=$\frac{3π}{4}$,OA=6,M为边AB上一点,M到边OA,OB的距离分别为2,2$\sqrt{2}$,则AB的长为6$\sqrt{5}$.
分析 利用面积法求出OB=6$\sqrt{2}$,再根据余弦定理即可求出
解答 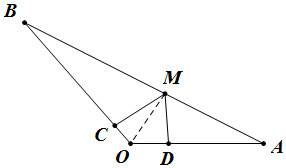 解:如图所示,由题意可得MC=2$\sqrt{2}$,MD=2,且MC⊥OB,MD⊥OA,
解:如图所示,由题意可得MC=2$\sqrt{2}$,MD=2,且MC⊥OB,MD⊥OA,
∵S△AOB=S△MOB+S△AOM,
∴$\frac{1}{2}$OA•OB•sin∠AOB=$\frac{1}{2}$OB•MC+$\frac{1}{2}$OA•MD,
即6×$\frac{\sqrt{2}}{2}$OB=2$\sqrt{2}$OB+6×2,
解得OB=6$\sqrt{2}$,
由余弦定理可得AB2=OB2+OA2-2OB•OA•cos∠AOB=72+36-2×6$\sqrt{2}$×6×(-$\frac{\sqrt{2}}{2}$)=180,
∴AB=6$\sqrt{5}$,
故答案为:6$\sqrt{5}$.
点评 本题考查了三角形的面积公式和余弦定理,考查了学生的运算能力,属于中档题

练习册系列答案
相关题目
1.一个几何体的三视图如图所示,其中俯视图为正方形,则该几何体最大的侧面的面积为( )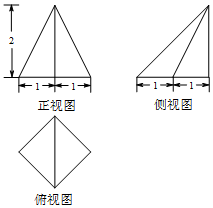

| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
5.某几何体的三视图如图所示,则该几何体的体积为( )
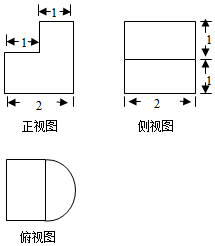

| A. | $\frac{1}{2}+\frac{π}{2}$ | B. | $1+\frac{π}{2}$ | C. | 1+π | D. | 2+π |
19.在复平面内,复数z=$\frac{2i}{1+i}$(i为虚数单位)的共轭复数对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
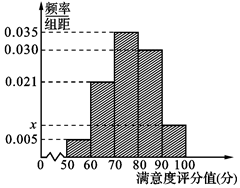 共享单车是指由企业在校园、公交站点、商业区、公共服务区等场所提供的自行车单车共享服务,由于其依托“互联网+”,符合“低碳出行”的理念,已越来越多地引起了人们的关注.某部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照 分成5组,制成如图所示频率分直方图.
共享单车是指由企业在校园、公交站点、商业区、公共服务区等场所提供的自行车单车共享服务,由于其依托“互联网+”,符合“低碳出行”的理念,已越来越多地引起了人们的关注.某部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照 分成5组,制成如图所示频率分直方图.