题目内容
18.甲、乙、丙三位同学同时参加M项体育比赛,每项比赛第一名、第二名、第三名得分分别为p1,p2,p3(p1>p2>p3,p1,p2,p3∈N*,比赛没有并列名次),比赛结果甲得22分,乙、丙都得9分,且乙有一项得第一名,则M的值为2,3,4,5.分析 M=1时不成立.M=2时,假设第一项比赛得分分别为:乙8甲7丙6,则另一项比赛得分分别为:甲15丙3乙1.满足条件.同理可得:M=3,4,5满足条件.M≥6时,不可能满足条件.
解答 解:M=1时不成立.
M=2时,假设第一项比赛得分分别为:乙8甲7丙6,则另一项比赛得分分别为:甲15丙3乙1.满足条件.
M=3时,可能三项得分分别为:乙7甲6丙5,甲8丙2乙1,甲8丙2乙1,满足条件.
M=4时,可能三项得分分别为:乙6甲5丙2,甲6丙3乙1,甲6丙2乙1,甲5丙2乙1,满足条件.
M=5时,可能三项得分分别为:乙5甲4丙1,甲5丙2乙1,甲5丙2乙1,甲4丙2乙1,甲4丙2乙1,满足条件.
M≥6时,不可能满足条件.
综上可得:M的值可为:2,3,4,5.
故答案为:2,3,4,5.
点评 本题考查了合情推理、分类讨论方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
9.定义在R上的可导函数f(x),其导函数记为f'(x),满足f(x)+f(2-x)=(x-1)2,且当x≤1时,恒有f'(x)+2<x.若$f(m)-f({1-m})≥\frac{3}{2}-3m$,则实数m的取值范围是( )
| A. | (-∞,1] | B. | $({-\frac{1}{3},1}]$ | C. | [1,+∞) | D. | $({-∞,\frac{1}{2}}]$ |
6.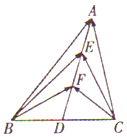 如图.在△ABC中,D是BC的中点,E、F是AD上的两个三等分点,$\overrightarrow{BA}$•$\overrightarrow{CA}$=4,$\overrightarrow{BF}$•$\overrightarrow{CF}$=-1,则$\overrightarrow{BE}$•$\overrightarrow{CE}$的值是( )
如图.在△ABC中,D是BC的中点,E、F是AD上的两个三等分点,$\overrightarrow{BA}$•$\overrightarrow{CA}$=4,$\overrightarrow{BF}$•$\overrightarrow{CF}$=-1,则$\overrightarrow{BE}$•$\overrightarrow{CE}$的值是( )
 如图.在△ABC中,D是BC的中点,E、F是AD上的两个三等分点,$\overrightarrow{BA}$•$\overrightarrow{CA}$=4,$\overrightarrow{BF}$•$\overrightarrow{CF}$=-1,则$\overrightarrow{BE}$•$\overrightarrow{CE}$的值是( )
如图.在△ABC中,D是BC的中点,E、F是AD上的两个三等分点,$\overrightarrow{BA}$•$\overrightarrow{CA}$=4,$\overrightarrow{BF}$•$\overrightarrow{CF}$=-1,则$\overrightarrow{BE}$•$\overrightarrow{CE}$的值是( )| A. | 4 | B. | 8 | C. | $\frac{7}{8}$ | D. | $\frac{3}{4}$ |
7.已知$sinα=\frac{{\sqrt{10}}}{10}$,$sin(α-β)=-\frac{{\sqrt{5}}}{5}$,$α,β∈(0,\frac{π}{2})$,则β=( )
| A. | $\frac{5π}{12}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
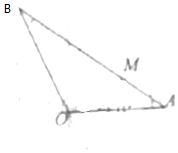 如图,在△AOB中,∠AOB=$\frac{3π}{4}$,OA=6,M为边AB上一点,M到边OA,OB的距离分别为2,2$\sqrt{2}$,则AB的长为6$\sqrt{5}$.
如图,在△AOB中,∠AOB=$\frac{3π}{4}$,OA=6,M为边AB上一点,M到边OA,OB的距离分别为2,2$\sqrt{2}$,则AB的长为6$\sqrt{5}$.