题目内容
5．某几何体的三视图如图所示，则该几何体的体积为（ ）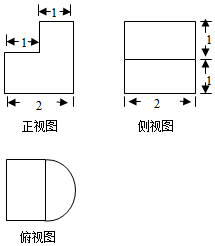
| A． | $\frac{1}{2}+\frac{π}{2}$ | B． | $1+\frac{π}{2}$ | C． | 1+π | D． | 2+π |
分析 由根据三视图可得该几何体为一个长方体和半个圆柱组合所成，由此求出几何体的体积，
解答 
解：根据三视图可得该几何体为一个长方体和半个圆柱组合所成，
所以体积V=1×1×2+$\frac{1}{2}$×π×12×2=2+π，
故选：D
点评 本题考查三视图求几何体的体积，由三视图正确复原几何体是解题的关键，考查空间想象能力．
练习册系列答案
名校通行证有效作业系列答案
相关题目
8．若函数f（x）=sinx+3|sinx|在x∈[0，2π]与直线y=2a有两个交点，则a的取值范围为（ ）
| A． | （2，4） | B． | （1，3） | C． | （1，2） | D． | （2，3） |
16．
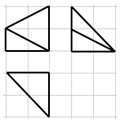某几何体的三视图如图所示（网格线中，每个小正方形的边长为1），则该几何体的体积为（ ）
某几何体的三视图如图所示（网格线中，每个小正方形的边长为1），则该几何体的体积为（ ）| A． | 2 | B． | 3 | C． | 4 | D． | 6 |
如图，网格纸的小正方形的边长是1，粗线表示一正方体被某平面截得的几何体的三视图，则该几何体的体积为（ ）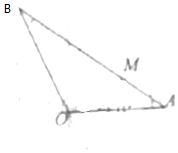
如图，在△AOB中，∠AOB=$\frac{3π}{4}$，OA=6，M为边AB上一点，M到边OA，OB的距离分别为2，2$\sqrt{2}$，则AB的长为6$\sqrt{5}$．
《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有刍甍，下广三丈，袤四丈，上袤二丈，无广，高一丈．问积几何？”其意思为：“今有底面为矩形的屋脊状的楔体，下底面宽3丈，长4丈，上棱长2丈，无宽，高1丈．现给出该楔体的三视图，其中网格纸上小正方形的边长为1丈，则该楔体的体积为（ ）