题目内容
已知函数f(x)=x2+(4-2a)x+a2+1.
(1)若函数f(x)在[1,+∞)上单调递增,求实数a的取值范围;
(2)设P=
[f(x1)+f(x2)],Q=f (
).试比较P与Q的大小;
(3)是否存在实数a∈[-8,0],使得函数f(x)在区间[-4,0]上的最小值为-7?若存在,求出a的值;若不存在,请说明理由.
(1)若函数f(x)在[1,+∞)上单调递增,求实数a的取值范围;
(2)设P=
| 1 |
| 2 |
| x1+x2 |
| 2 |
(3)是否存在实数a∈[-8,0],使得函数f(x)在区间[-4,0]上的最小值为-7?若存在,求出a的值;若不存在,请说明理由.
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:函数的性质及应用
分析:(1)函数f(x)=x2+(4-2a)x+a2+1为二次函数,开口向上,对称轴为 x=a-2,由此能求出实数a的取值范围.
(2)作差得P-Q=
[f(x1)+f(x2)-f (
)=
>0,由此得到P>Q.
(3)设存在这样的a,由于-8≤a≤0,所以-10≤a-2≤-2,由此结合对称轴利用函数的单调性能求出存在a=-1满足条件.
(2)作差得P-Q=
| 1 |
| 2 |
| x1+x2 |
| 2 |
| (x1-x2)2 |
| 4 |
(3)设存在这样的a,由于-8≤a≤0,所以-10≤a-2≤-2,由此结合对称轴利用函数的单调性能求出存在a=-1满足条件.
解答:
解:(1)函数f(x)=x2+(4-2a)x+a2+1为二次函数,
开口向上,对称轴为 x=a-2,
要使函数在[1,+∞)上单调递增,则对称轴必在x=1的右侧,
即a-2≥1,解得a≥3.
∴实数a的取值范围是[3,+∞).
(2)P-Q=
[f(x1)+f(x2)-f (
)
=
[x12+(4-2a)x1+a2+1+x22+(4-2a)x2+a2+1]-[
+
(4-2a)(x1+x2)+a2+1]
=
-
=
>0,
∴P>Q.
(3)设存在这样的a,
由于-8≤a≤0,∴-10≤a-2≤-2,
若-10≤a-2<-4,即-8≤a<-2,则f(x) 在[-4,0]上为减函数,
∴f(0)=a2+1=-7,
无解;
若-4≤a-2≤-2,即-2≤a≤0,
则f(a-2)=(a-2)2+(4-2a)(a-2)+a2+1=-7,
化简得4a+4=0,解得 a=-1,
综上,存在a=-1满足条件.
开口向上,对称轴为 x=a-2,
要使函数在[1,+∞)上单调递增,则对称轴必在x=1的右侧,
即a-2≥1,解得a≥3.
∴实数a的取值范围是[3,+∞).
(2)P-Q=
| 1 |
| 2 |
| x1+x2 |
| 2 |
=
| 1 |
| 2 |
| (x1+x2)2 |
| 4 |
| 1 |
| 2 |
=
| x12+x22 |
| 2 |
| (x1+x2)2 |
| 4 |
| (x1-x2)2 |
| 4 |
∴P>Q.
(3)设存在这样的a,
由于-8≤a≤0,∴-10≤a-2≤-2,
若-10≤a-2<-4,即-8≤a<-2,则f(x) 在[-4,0]上为减函数,
∴f(0)=a2+1=-7,
无解;
若-4≤a-2≤-2,即-2≤a≤0,
则f(a-2)=(a-2)2+(4-2a)(a-2)+a2+1=-7,
化简得4a+4=0,解得 a=-1,
综上,存在a=-1满足条件.
点评:本题考查实数的取值范围的求法,考查两数大小的比较,考查满足条件的实数值是否存在的判断与求法,解题时要注意二次函数性质的合理运用.

练习册系列答案
相关题目
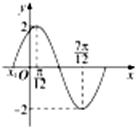 已知函数f(x)=Asin(ωx+φ)在一个周期内的图象如图所示.
已知函数f(x)=Asin(ωx+φ)在一个周期内的图象如图所示.