题目内容
12.在△ABC中,AB=5,AC=7,∠A=60°,G是重心,过G的平面α与BC平行,AB∩α=M,AC∩α=N,则MN=( )| A. | $\frac{8}{3}$ | B. | $\frac{3}{8}$ | C. | $\frac{4}{3}$ | D. | $\frac{{2\sqrt{39}}}{3}$ |
分析 由已知AB=5,AC=7,∠A=60°利用余弦定理可求BC,根据线面平行的性质定理可得,MN∥BC,且G是△ABC的重心可得MN=$\frac{2}{3}$BC,从而可求MN.
解答 解:如图,在△ABC中,由余弦定理知BC=$\sqrt{25+49-2×5×7×\frac{1}{2}}$=$\sqrt{39}$,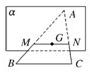
∵BC∥α,AB∩α=M,AC∩α=N,
根据线面平行的性质定理可得,MN∥BC,
又G是△ABC的重心,
∴MN=$\frac{2}{3}$BC=$\frac{2\sqrt{39}}{3}$.
故选:D.
点评 本题主要考查了余弦定理解决三角形中两边和夹角求第三边,直线与平面平行的性质定理的运用,三角形的重心的性质等知识的运用.

练习册系列答案
相关题目
20.数列{an}是以a1=1为首项,以2为公差的等差数列,若数列{$\frac{1}{{{a_n}{a_{n+1}}}}$}的前n项和为Tn,则满足Tn>$\frac{100}{209}$的最小正整数n为( )
| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
17.若不等式x2+a|x|+1≥0对x∈[-$\frac{1}{2}$,$\frac{1}{2}}$]恒成立,则实数a的取值范围是( )
| A. | [-2,+∞) | B. | [-2,2] | C. | (-∞,-2] | D. | [-$\frac{5}{2}$,+∞) |
4.方程|x2-4x+3|=a有且仅有三个不等实数根,则实数a满足( )
| A. | a=1 | B. | a>1或a=0 | C. | 0<a≤1 | D. | 0<a<1 |
