题目内容
2．已知等差数列{an}满足：d≠0，a10=5，Sk+3-Sk=15，则k=8．分析 Sk+3-Sk=15，即ak+1+ak+2+ak+3=15，利用通项公式即可得出．
解答 解：∵Sk+3-Sk=15，∴ak+1+ak+2+ak+3=15，
∴3a1+（3k+3）d=15，
可得a1+（k+1）d=5=a10，
∴k+2=10，解得k=8．
故答案为：8．
点评 本题考查了等差数列的通项公式及其性质，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
12．在△ABC中，AB=5，AC=7，∠A=60°，G是重心，过G的平面α与BC平行，AB∩α=M，AC∩α=N，则MN=（ ）
| A． | $\frac{8}{3}$ | B． | $\frac{3}{8}$ | C． | $\frac{4}{3}$ | D． | $\frac{{2\sqrt{39}}}{3}$ |
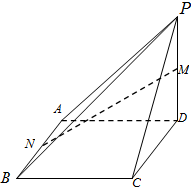如图：在四棱锥P-ABCD中，底面ABCD是矩形，PD⊥平面ABCD，且PD=DA=DC=2．