题目内容
4.方程|x2-4x+3|=a有且仅有三个不等实数根,则实数a满足( )| A. | a=1 | B. | a>1或a=0 | C. | 0<a≤1 | D. | 0<a<1 |
分析 把问题转化为函数y=|x2-4x+3|与直线y=a有3个交点,画出图象即可解决问题.
解答  解:∵方程|x2-4x+3|=a有三个实数根,
解:∵方程|x2-4x+3|=a有三个实数根,
∴可以看成函数y=|x2-4x+3|与直线y=a有3个交点即可.
函数y=|x2-4x+3|的图象如图所示,
∵y′=x2-4x+3的顶点D坐标为(2,-1),D关于x轴对称点的坐标D′(2,1),
由图象可知,a=1时,函数y=|x2-4x+3|与直线y=a有3个交点,
∴a=1.
故选:A.
点评 本题考查二次函数与x轴交点问题,解题的关键是画出函数y=|x2-4x+3|的图象,利用图象法解决问题,属于常考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.已知两个球的表面积之比为1:3,则这两个球的体积之比为( )
| A. | 1:9 | B. | 1:3$\sqrt{3}$ | C. | 1:3 | D. | 1:$\sqrt{3}$ |
12.在△ABC中,AB=5,AC=7,∠A=60°,G是重心,过G的平面α与BC平行,AB∩α=M,AC∩α=N,则MN=( )
| A. | $\frac{8}{3}$ | B. | $\frac{3}{8}$ | C. | $\frac{4}{3}$ | D. | $\frac{{2\sqrt{39}}}{3}$ |

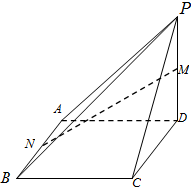 如图:在四棱锥P-ABCD中,底面ABCD是矩形,PD⊥平面ABCD,且PD=DA=DC=2.
如图:在四棱锥P-ABCD中,底面ABCD是矩形,PD⊥平面ABCD,且PD=DA=DC=2.