题目内容
设随机变量ξ~N(0,1),记Φ(x)=P(ξ<x),则P(-1<ξ<1)等于( )
| A、2Φ(1)-1 | ||
| B、2Φ(-1)-1 | ||
C、
| ||
| D、Φ(1)+Φ(-1) |
考点:离散型随机变量的期望与方差
专题:概率与统计
分析:由题意知P(-1<ξ<1)=P(ξ<1)-P(ξ<-1)=P(ξ<1)-[1-P(ξ<1)],由此能求出结果.
解答:
解:由题意知:
P(-1<ξ<1)
=P(ξ<1)-P(ξ<-1)
=P(ξ<1)-[1-P(ξ<1)]
=Φ(1)-[1-Φ(1)]
=2Φ(1)-1.
故选:A.
P(-1<ξ<1)
=P(ξ<1)-P(ξ<-1)
=P(ξ<1)-[1-P(ξ<1)]
=Φ(1)-[1-Φ(1)]
=2Φ(1)-1.
故选:A.
点评:本题考查正态曲线的特点及曲线所表示的意义,本题解题的关键是读懂条件中所给的一个新定义的式子.

练习册系列答案
相关题目
函数f (x)=|2x-a|+1 的定义域为[p,q],值域为[1,2],则q-p的最大值为( )
| A、1 | B、2 |
| C、a+1 | D、2 a |
已知数列{an}满足a1>0,且an+1=
an,则数列{an}是( )
| 1 |
| 2 |
| A、递增数列 | B、递减数列 |
| C、常数列 | D、摆动数列 |
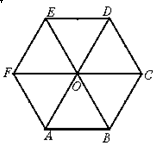 如图,设O是正六边形ABCDEF的中心,在向量
如图,设O是正六边形ABCDEF的中心,在向量| OB |
| OC |
| OD |
| OE |
| OF |
| AB |
| BC |
| CD |
| EF |
| DE |
| FA |
| OA |
| A、1个 | B、2个 | C、3个 | D、4个 |
从点P(1,-2)引圆(x+1)2+(y-1)2=4的切线,则切线长是( )
| A、4 | B、3 | C、2 | D、1 |