题目内容
已知复数z=1-2i（i为虚数单位）
（Ⅰ）把复数z的共轭复数记作
，若
•z1=4+3i，求复数z1；
（Ⅱ）已知z是关于x的方程2x2+px+q=0的一个根，求实数p，q的值．
（Ⅰ）把复数z的共轭复数记作
. |
| z |
. |
| z |
（Ⅱ）已知z是关于x的方程2x2+px+q=0的一个根，求实数p，q的值．
考点：虚数单位i及其性质
专题：数系的扩充和复数
分析：（I）利用复数的运算法则即可得出；
（II）利用实系数一元二次方程虚根成对原理、根与系数的关系即可得出．
（II）利用实系数一元二次方程虚根成对原理、根与系数的关系即可得出．
解答：
解：（Ⅰ）由题意得
=1+2i，
∴z1=
=
=
=2-i．
（Ⅱ）∵z是关于x的方程2x2+px+q=0的一个根，
则
也是关于x的方程2x2+px+q=0的一个根，
∴z+
=2=-
，z
=
，
解得p=-4，q=10．
. |
| z |
∴z1=
| 4+3i |
| 1+2i |
| (4+3i)(1-2i) |
| (1+2i)(1-2i) |
| 10-5i |
| 5 |
（Ⅱ）∵z是关于x的方程2x2+px+q=0的一个根，
则
. |
| z |
∴z+
. |
| z |
| p |
| 2 |
. |
| z |
| q |
| 2 |
解得p=-4，q=10．
点评：本题考查了复数的运算法则、实系数一元二次方程虚根成对原理、根与系数的关系、共轭复数的定义，考查了计算能力，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知x，y之间的一组数据如表所示，对于表中数据，现在给出如下拟合直线，则根据最小二乘法思想判断拟合程度最好的直线是（ ）
| x | 2 | 3 | 4 | 5 | 6 |
| y | 3 | 4 | 6 | 8 | 9 |
A、
| ||
B、
| ||
C、
| ||
D、
| ||
E、
|
设随机变量ξ～N（0，1），记Φ（x）=P（ξ＜x），则P（-1＜ξ＜1）等于（ ）
| A、2Φ（1）-1 | ||
| B、2Φ（-1）-1 | ||
C、
| ||
| D、Φ（1）+Φ（-1） |
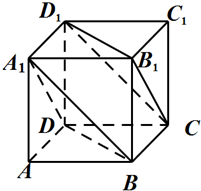如图，在正方体ABCD-A1B1C1D1中．