题目内容
已知一元二次方程ax2+bx+c=0的两根x1,x2分别是一元二次方程cx2+dx+a=0的两根的2013倍,试证明:|b|=|d|.
考点:一元二次方程的根的分布与系数的关系
专题:函数的性质及应用
分析:根据一元二次方程根与系数之间的关系,即可得到结论.
解答:
解:∵一元二次方程ax2+bx+c=0的两根x1,x2,
∴x1+x2=-
,x1x2=
,
∵x1,x2分别是一元二次方程cx2+dx+a=0的两根的2013倍,
∴一元二次方程cx2+dx+a=0的两根分别为
,
,
则
+
=-
,
•
=
,
即x1+x2=-
×2013,x1x2=20132•
,
则-
×2013=-
,x1x2=20132•
=
,
即2013ad=bc,20132•a2=c2,
则c=±2013a,
2013ad=bc=±2013ab,
则b=±d成立.
即b|=|d|成立.
∴x1+x2=-
| b |
| a |
| c |
| a |
∵x1,x2分别是一元二次方程cx2+dx+a=0的两根的2013倍,
∴一元二次方程cx2+dx+a=0的两根分别为
| x1 |
| 2013 |
| x2 |
| 2013 |
则
| x1 |
| 2013 |
| x2 |
| 2013 |
| d |
| c |
| x1 |
| 2013 |
| x2 |
| 2013 |
| a |
| c |
即x1+x2=-
| d |
| c |
| a |
| c |
则-
| d |
| c |
| b |
| a |
| a |
| c |
| c |
| a |
即2013ad=bc,20132•a2=c2,
则c=±2013a,
2013ad=bc=±2013ab,
则b=±d成立.
即b|=|d|成立.
点评:本题主要考查一元二次方程根与关系的应用,要求熟练掌握根与系数之间的关系.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
f(x)=(a+2b)x+2a-b(a≥0),且当x∈[0,1]时恒有f(x)≤1,则f(-1)的最大值为( )
| A、3 | B、-3 | C、6 | D、-6 |
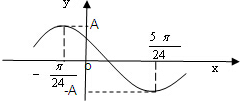 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),其部分图象如图所示,且直线y=A与曲线y=f(x)(-
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),其部分图象如图所示,且直线y=A与曲线y=f(x)(-
 如图,平行四边形ABCD的对角线AC∩BD=0,且AB=BC=BD=6,BM=MC,将四边形ABCD沿对角线AC折起,得到三棱锥B-ACD,且DM=3
如图,平行四边形ABCD的对角线AC∩BD=0,且AB=BC=BD=6,BM=MC,将四边形ABCD沿对角线AC折起,得到三棱锥B-ACD,且DM=3 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,且PA⊥底面ABCD,BD⊥PC,E是PA的中点.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,且PA⊥底面ABCD,BD⊥PC,E是PA的中点.