题目内容
在平面上给定一个△ABC，试判断平面上是否存在这样的点P，使得线段AP的中点为M，线段BM的中点为N，线段CN的中点为P？若存在，这样的点P有几个？若不存在，说明理由．
考点：空间中直线与平面之间的位置关系
专题：空间位置关系与距离
分析：平面上是否存在这样的点P，只有一个．作l∥AC，使l与AC的距离等于AC上高的
，作m∥BC，使m与BC距离等于BC上高的
，交点为P，点P为所求的点．
| 2 |
| 7 |
| 1 |
| 7 |
解答：
解：平面上是否存在这样的点P，只有一个．
作l∥AC，使l与AC的距离等于AC上高的
，
作m∥BC，使m与BC距离等于BC上高的
，交点为P，
AP中点M，连结BM，连结CP，延长交BM于N，
则点P为所求的点．
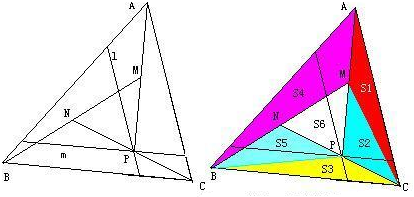
证明：如图，S1=S2=
S△ABC=S3，
S4=S5+S6=
=
，
S2，S3同底PC，它们在PC上的高相等，
S2，S3在PC上的高相等，也是S5，S6在PN上的高，
S5=S6=
，
S5，S6的高=P到BM的距离，故BM=MN，
S5=S3，故CP=PN．
作l∥AC，使l与AC的距离等于AC上高的
| 2 |
| 7 |
作m∥BC，使m与BC距离等于BC上高的
| 1 |
| 7 |
AP中点M，连结BM，连结CP，延长交BM于N，
则点P为所求的点．
证明：如图，S1=S2=
| 1 |
| 7 |
S4=S5+S6=
1-
| ||
| 2 |
| 2 |
| 7 |
S2，S3同底PC，它们在PC上的高相等，
S2，S3在PC上的高相等，也是S5，S6在PN上的高，
S5=S6=
| 1 |
| 7 |
S5，S6的高=P到BM的距离，故BM=MN，
S5=S3，故CP=PN．
点评：本题考查满足条件的点的判断与求法，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
阅读快车系列答案
相关题目
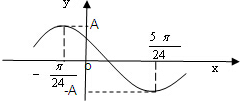已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π），其部分图象如图所示，且直线y=A与曲线y=f（x）（-
如图，在四棱锥P-ABCD中，底面ABCD是平行四边形，且PA⊥底面ABCD，BD⊥PC，E是PA的中点．