题目内容
已知数列{an}的前n项和Sn=
n2+pn,数列{bn}的前n项和为Tn=2n-1,且a4=b4.
(Ⅰ)求数列{an}、{bn}的通项公式;
(Ⅱ)若对于数列{cn}有cn=2an•bn,请求出数列{cn}的前n项和Rn.
| 1 |
| 2 |
(Ⅰ)求数列{an}、{bn}的通项公式;
(Ⅱ)若对于数列{cn}有cn=2an•bn,请求出数列{cn}的前n项和Rn.
考点:数列的求和,等差数列的性质
专题:等差数列与等比数列
分析:(Ⅰ)由已知条件根据a4=b4,求出p=
.由an=
,能求出数列{an}、{bn}的通项公式.
(2)cn=2an•bn=(n+4)×2n,由此利用错位相减法能求出数列{cn}的前n项和Rn.
| 9 |
| 2 |
|
(2)cn=2an•bn=(n+4)×2n,由此利用错位相减法能求出数列{cn}的前n项和Rn.
解答:
解:(Ⅰ)∵数列{an}的前n项和Sn=
n2+pn,
数列{bn}的前n项和为Tn=2n-1,且a4=b4,
∴a4=S4-S3=(
×16+4p)-(
×9+3p)=
+p,
b4=T4-T3=15-7=8,
∵a4=b4,∴
+p=8,解得p=
.
∴Sn=
n2+
n,
∴a1=S1=5,an=Sn-Sn-1=[(
n2+
n)-(
(n-1)2+
(n-1)=n+4,(n≥2)
∵a1=5=1+4
∴数列{an}的通项公式为an=n+4.
∵Tn=2n-1,
∴b1=T1=1,Tn-1=2n-1-1,(n≥2)
∴bn=Tn-Tn-1=(2n-1)-(2n-1-1)=2n-1,(n≥2)
∵b1=1=21-1,
∴数列{bn}的通项公式为bn=2n-1.
(2)cn=2an•bn=(n+4)×2n,
则Rn=5×2+6×22+7×23+…+(n+4)×2n
2Rn=5×22+6×23+…+(n+3)×2n+(n+4)×2n+1,
两式相减:-Rn=10+22+23+…+2n-(n+4)×2n+1
=10+
-(n+4)×2n+1
=6-(n+3)×2n+1,
∴Rn=(n+3)×2n+1-6.
| 1 |
| 2 |
数列{bn}的前n项和为Tn=2n-1,且a4=b4,
∴a4=S4-S3=(
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| 2 |
b4=T4-T3=15-7=8,
∵a4=b4,∴
| 7 |
| 2 |
| 9 |
| 2 |
∴Sn=
| 1 |
| 2 |
| 9 |
| 2 |
∴a1=S1=5,an=Sn-Sn-1=[(
| 1 |
| 2 |
| 9 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
∵a1=5=1+4
∴数列{an}的通项公式为an=n+4.
∵Tn=2n-1,
∴b1=T1=1,Tn-1=2n-1-1,(n≥2)
∴bn=Tn-Tn-1=(2n-1)-(2n-1-1)=2n-1,(n≥2)
∵b1=1=21-1,
∴数列{bn}的通项公式为bn=2n-1.
(2)cn=2an•bn=(n+4)×2n,
则Rn=5×2+6×22+7×23+…+(n+4)×2n
2Rn=5×22+6×23+…+(n+3)×2n+(n+4)×2n+1,
两式相减:-Rn=10+22+23+…+2n-(n+4)×2n+1
=10+
| 4(1-2n-1) |
| 1-2 |
=6-(n+3)×2n+1,
∴Rn=(n+3)×2n+1-6.
点评:本题考查数列的通项公式的求法,考查数列的前n项和的求法,解题时要认真审题,注意错位相减法的合理运用.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
下列所示的图形中,可以作为函数y=f(x)的图象的是( )
A、 |
B、 |
C、 |
D、 |
阅读如图所示程序:

若输出y=9,则输入的x值应该是( )

若输出y=9,则输入的x值应该是( )
| A、-1 | B、4或-1 |
| C、4 | D、2或-2 |
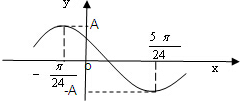 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),其部分图象如图所示,且直线y=A与曲线y=f(x)(-
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),其部分图象如图所示,且直线y=A与曲线y=f(x)(-| π |
| 24 |
| 11π |
| 24 |
| π |
| 8 |
| 2π |
| 8 |
| 3π |
| 8 |
| 2014π |
| 8 |
| 2014 |
 |
| i=1 |
| i•π |
| 8 |
| A、0 | ||
B、-1-
| ||
| C、-1 | ||
D、-1+
|
函数f(x)=(x2-2x)ex(e为自然数的底数)的图象大致是( )
A、 |
B、 |
C、 |
D、 |
 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,且PA⊥底面ABCD,BD⊥PC,E是PA的中点.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,且PA⊥底面ABCD,BD⊥PC,E是PA的中点.