题目内容
设f（x）与g（x）是定义在同一区间[m，n]上的两个函数，若函数y=f（x）+g（x）在x∈[m，n]上有两个不同的零点，则称f（x）和g（x）在[m，n]上是“相互函数”；若f（x）=-4lnx-5x与g（x）=x2+3x+a在区间[1，e]上是相互函数，则a的取值范围为（ ）
| A、[1，4ln2） |
| B、[-e2+2e+4，4ln2） |
| C、（4ln2，+∞） |
| D、[1，-e2+2e+4] |
考点：函数零点的判定定理,进行简单的合情推理
专题：函数的性质及应用
分析：先求出y的表达式，由题意解不等式组求出 即可．
解答：
解：∵y=f（x）+g（x）=-4lnx-5x+x2+3x+a，
∴x=1时，y=a-1≥0，解得：a≥1①
x=e时，y=e2-2e-4+a≥0，解得：a≥-e2+2e+4②，
x=2时，y=-4ln2+a＜0，解得：a＜4ln2③，
综合①②③得：-e2+2e+4≤a＜4ln2，
故选：B．
∴x=1时，y=a-1≥0，解得：a≥1①
x=e时，y=e2-2e-4+a≥0，解得：a≥-e2+2e+4②，
x=2时，y=-4ln2+a＜0，解得：a＜4ln2③，
综合①②③得：-e2+2e+4≤a＜4ln2，
故选：B．
点评：本题考察了函数的零点问题，新定义问题，不等式的解法，是一道基础题．
练习册系列答案
全能测控期末小状元系列答案
相关题目
已知复数z=
（i是虚数单位），则z的共轭复数
=（ ）
| 2 |
| 1-i |
. |
| z |
| A、1+i | B、1-i |
| C、-1+i | D、-1-i |
阅读如图所示程序：
若输出y=9，则输入的x值应该是（ ）
若输出y=9，则输入的x值应该是（ ）
| A、-1 | B、4或-1 |
| C、4 | D、2或-2 |
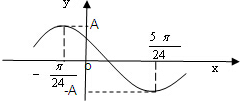已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π），其部分图象如图所示，且直线y=A与曲线y=f（x）（-| π |
| 24 |
| 11π |
| 24 |
| π |
| 8 |
| 2π |
| 8 |
| 3π |
| 8 |
| 2014π |
| 8 |
| 2014 |
 |
| i=1 |
| i•π |
| 8 |
| A、0 | ||
B、-1-
| ||
| C、-1 | ||
D、-1+
|
函数f（x）=（x2-2x）ex（e为自然数的底数）的图象大致是（ ）
A、 |
B、 |
C、 |
D、 |