题目内容

等差数列数列{an}的公差为2，前n项和为Sn，若a1，a3，a4成等比数列，则S20=（　　）
A、180B、220
C、580D、410
考点：数列的求和
专题：等差数列与等比数列
分析：由已知条件利用等差数列的通项公式和等比数列性质求出a1=-8，由此能求出S20的值．
解答： 解：∵等差数列数列{an}的公差为2，前n项和为Sn，
a1，a3，a4成等比数列，
∴（a1+4）2=a1•（a1+6），
解得a1=-8，
∴S20=20×（-8）+
20×19
2
×2=220．
故选：B．
点评：本题考查数列的前20项和的求法，是基础题，解题时要注意等差数列和等比数列的性质的灵活运用．
练习册系列答案
相关题目
已知函数f（x）=lnx-ax2+x有两个不同的零点，则实数a的取值范围是
 
．
下列所示的图形中，可以作为函数y=f（x）的图象的是（　　）
A、
B、
C、
D、
f（x）=（a+2b）x+2a-b（a≥0），且当x∈[0，1]时恒有f（x）≤1，则f（-1）的最大值为（　　）
A、3B、-3C、6D、-6
已知复数z=
2
1-i
（i是虚数单位），则z的共轭复数
.
z
=（　　）
A、1+iB、1-i
C、-1+iD、-1-i
已知△ABC中，a=
6
，b=2，B=45°，则角A等于（　　）
A、30°B、90°
C、60°D、60°或120°
阅读如图所示程序：

若输出y=9，则输入的x值应该是（　　）
A、-1B、4或-1
C、4D、2或-2
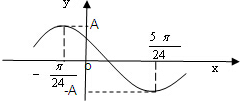已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π），其部分图象如图所示，且直线y=A与曲线y=f（x）（-
π
24
≤x≤
11π
24
）所围成的封闭图形的面积为π，则f（
π
8
）+f（
2π
8
）+f（
3π
8
）+…+f（
2014π
8
）（即
2014
i=1
f（
i•π
8
））的值为（　　）
A、0
B、-1-
3
C、-1
D、-1+
3
如图，在四棱锥P-ABCD中，底面ABCD是平行四边形，且PA⊥底面ABCD，BD⊥PC，E是PA的中点．
（Ⅰ）求证：平面PAC⊥平面EBD；
（Ⅱ）若PA=AB=AC=2，求三棱锥P-EBD的体积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网