题目内容
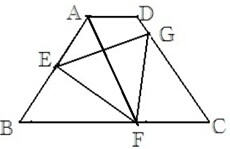 如图,梯形ABCD,AD∥BC,AB=CD=6,AD=2,BC=8,∠B=60°,点E在AB上,点F在BC上,
如图,梯形ABCD,AD∥BC,AB=CD=6,AD=2,BC=8,∠B=60°,点E在AB上,点F在BC上,(1)若点G在CD上,△DEF是等边三角形,设BE=x,△GEF的边长为y,求y关于x的函数解析式,并写出定义域;
(2)在第(1)小题中,连结AF,若AF⊥EG,求BE的长.
考点:解三角形,函数解析式的求解及常用方法
专题:函数的性质及应用,解三角形
分析:(1)由已知,三角形EFG是等边三角形,设∠EFB=α,则∠BEF=120°-α;而∠GFC=120°-α,且∠B=∠C=60°,所以∠FGC=α,又EF=FG,由此可知三角形BEF与三角形GF;所以FC=EB=x,则在三角形BEF中,运用余弦定理可得y与x的关系式;当G与D重合时,可知x最小,E与A重合时,x最大,据此得定义域;
(2)由(1)知,BE=x,BF=8-x,结合∠B=60°,在直角三角形BEF中,x可求.
(2)由(1)知,BE=x,BF=8-x,结合∠B=60°,在直角三角形BEF中,x可求.
解答:
解:(1)由已知,∠B=∠C,设∠BFE=α,则∠BEF=∠GFC=120°-α,且EF=FG=y,
所以△BEF≌△CFG,所以BE=FC=x,BF=8-x
在三角形BEF中由余弦定理得EF2=BE2+BF2-2BE•BFcosB,
即y2=x2+(8-x)2-2x(8-x)cos60°,化简得:
y=
,x∈[2,6].
(2)若EG⊥AF,则AF垂直平分EG,连接AG,则AG=AE=6-x,
又由(1)知CG=BF=8-x,所以DG=6-(8-x)=x-2,AD=2,
则在三角形ADG中,∠ADG=120°,
所以由余弦定理得AG2=AD2+DG2-2AD•DGcos120°,即(6-x)2=4+(x-2)2-2×2(x-2)cos120°,
解得x=
,所以BE的长为
.
所以△BEF≌△CFG,所以BE=FC=x,BF=8-x
在三角形BEF中由余弦定理得EF2=BE2+BF2-2BE•BFcosB,
即y2=x2+(8-x)2-2x(8-x)cos60°,化简得:
y=
| 3x2-24x+64 |
(2)若EG⊥AF,则AF垂直平分EG,连接AG,则AG=AE=6-x,
又由(1)知CG=BF=8-x,所以DG=6-(8-x)=x-2,AD=2,
则在三角形ADG中,∠ADG=120°,
所以由余弦定理得AG2=AD2+DG2-2AD•DGcos120°,即(6-x)2=4+(x-2)2-2×2(x-2)cos120°,
解得x=
| 16 |
| 5 |
| 16 |
| 5 |
点评:解决此题用到了平几的一些基础知识,注意复习回顾一下;同时解三角形要注意把所给的和所求的条件、结论尽量归到一个三角形中,再利用正余弦定理求解.

练习册系列答案
 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
设a∈R,若函数f(x)=ex-ax,x∈R有大于零的极值点,则( )
| A、a<1 | ||
| B、a>1 | ||
C、a<
| ||
D、a>
|
已知f(x)是可导的函数,且f′(x)<f(x)对于x∈R恒成立,则( )
| A、f(1)<ef(0),f(2015)>e2015f(0) |
| B、f(1)>ef(0),f(2015)>e2015f(0) |
| C、f(1)>ef(0),f(2015)<e2015f(0) |
| D、f(1)<ef(0),f(2015)<e2015f(0) |
某观察站C与两灯塔A、B的距离分别为300米和500米,测得灯塔A在观察站C北偏东30°,灯塔B在观察站C正西方向,则两灯塔A、B间的距离为( )
| A、500米 | B、600米 |
| C、700米 | D、800米 |
若-
<β<0<α<
,cos(
+α)=
,cos(
-
)=
,则cos(α+
)=( )
| π |
| 2 |
| π |
| 2 |
| π |
| 4 |
| 1 |
| 3 |
| π |
| 4 |
| β |
| 2 |
| ||
| 3 |
| β |
| 2 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|