题目内容
已知函数f(x)=
是R上的增函数,那么a的取值范围是 .
|
考点:函数单调性的性质
专题:函数的性质及应用
分析:由一次函数的性质,得不等式,解出即可.
解答:
解:∵函数f(x)是R上的增函数,
∴3-a>0,解得:a<3,
∵x=2时,2(3-a)-4a≤4,解得:a≥
故答案为:[
,3).
∴3-a>0,解得:a<3,
∵x=2时,2(3-a)-4a≤4,解得:a≥
| 1 |
| 3 |
故答案为:[
| 1 |
| 3 |
点评:本题考查了函数的单调性,本题属于基础题.

练习册系列答案
相关题目
双曲线
-y2=1的渐近线方程为( )
| x2 |
| 4 |
A、y=±
| ||
| B、y=±x | ||
| C、y=±2x | ||
| D、y=±4x |
下列命题中的假命题是( )
| A、?x∈R,21-x>0 | ||
B、?x∈(0,+∞),2x>x
| ||
| C、?x0∈R,当x>x0时,恒有1.1x<x4 | ||
| D、?α∈R,使函数 y=xα的图象关于y轴对称 |
设a∈R,则“a=1”是“直线l2:ax+y-1=0与直线l2:x-ay-3=0垂直”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
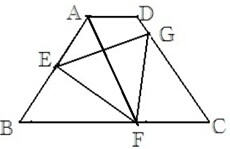 如图,梯形ABCD,AD∥BC,AB=CD=6,AD=2,BC=8,∠B=60°,点E在AB上,点F在BC上,
如图,梯形ABCD,AD∥BC,AB=CD=6,AD=2,BC=8,∠B=60°,点E在AB上,点F在BC上,