题目内容
若-
<β<0<α<
,cos(
+α)=
,cos(
-
)=
,则cos(α+
)=( )
| π |
| 2 |
| π |
| 2 |
| π |
| 4 |
| 1 |
| 3 |
| π |
| 4 |
| β |
| 2 |
| ||
| 3 |
| β |
| 2 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
考点:两角和与差的余弦函数
专题:三角函数的求值
分析:观察已知角与所求角之间的关系得到α+
=(
+α)-(
-
),只要再求出另一个三角函数值,利用两角差的余弦公式解答.
| β |
| 2 |
| π |
| 4 |
| π |
| 4 |
| β |
| 2 |
解答:
解:∵若-
<β<0<α<
,cos(
+α)=
,cos(
-
)=
,
∴sin(
+α)=
,sin(
-
)=
,
∴cos(α+
)=cos[(
+α)-(
-
)]=cos(
+α)cos(
-
)+sin(
+α)sin(
-
)=)=
×
+
×
=
;
故选C.
| π |
| 2 |
| π |
| 2 |
| π |
| 4 |
| 1 |
| 3 |
| π |
| 4 |
| β |
| 2 |
| ||
| 3 |
∴sin(
| π |
| 4 |
2
| ||
| 3 |
| π |
| 4 |
| β |
| 2 |
| ||
| 3 |
∴cos(α+
| β |
| 2 |
| π |
| 4 |
| π |
| 4 |
| β |
| 2 |
| π |
| 4 |
| π |
| 4 |
| β |
| 2 |
| π |
| 4 |
| π |
| 4 |
| β |
| 2 |
| 1 |
| 3 |
| ||
| 3 |
2
| ||
| 3 |
| ||
| 3 |
5
| ||
| 9 |
故选C.
点评:本题考查了三角函数求值中角的等价变换以及两角和与差的三角函数公式的运用,本题关键是发现α+
=(
+α)-(
-
).
| β |
| 2 |
| π |
| 4 |
| π |
| 4 |
| β |
| 2 |

练习册系列答案
相关题目
设a∈R,则“a=1”是“直线l2:ax+y-1=0与直线l2:x-ay-3=0垂直”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
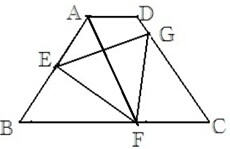 如图,梯形ABCD,AD∥BC,AB=CD=6,AD=2,BC=8,∠B=60°,点E在AB上,点F在BC上,
如图,梯形ABCD,AD∥BC,AB=CD=6,AD=2,BC=8,∠B=60°,点E在AB上,点F在BC上,