Question

设f（x）=ax²+b（a＞0，b＞0），对任意x、y都有f（xy）+f（x+y）≥f（x）•f（y），求点P（a，b）所在区域的面积．

Answer 1

考点：抽象函数及其应用

专题：函数的性质及应用

分析：已知条件可转化为：对任意实数x，y，有（ax²y²+b）+[a（x+y）²+b]≥（ax²+b）（ay²+b），由已知条件推导出所求的正实数对（a，b）全体为：{（a，b）|

0＜b≤1 0＜a＜1 2a+b≤2

}，作出可行域，得点P（a，b）所在区域为梯形OABC，由此能求出点P（a，b）所在区域的面积．

解答： 解：已知条件可转化为：对任意实数x，y，
有（ax²y²+b）+[a（x+y）²+b]≥（ax²+b）（ay²+b），①
先寻找a，b所满足的必要条件，
在①式中，令y=0，得b+（ax²+b）≥（ax²+b）•b，
即对任意实数x，y，有（1-b）ax²+b（2-b）≥0，
由于a＞0，故ax²能取到任意大的正值，
因此必有1-b≥0，即0＜b≤1．
在①式中再令y=-x，得（ax⁴+b）+b≥（ax²+b）²，
即对任意实数x，有（a-a²）x⁴-2abx²+（2b-b²）≥0，②
将②式的左边记为g（x），由题意，得a-a²≠0，
（否则，由a＞0知a=1，此时g（x）=-2bx²+（2b-b²），其中b＞0，故g（x）可取到负值，矛盾），
于是g（x）=（a-a²）（x²-

ab

a-a2

）²-

(ab)2

a-a2

+（2b-b²）
=（a-a²）（x²-

b

1-a

）²+

b

1-a

（2-2a-b）≥0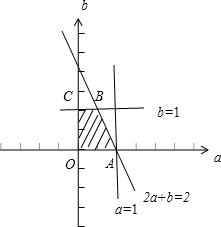
对一切实数成立，从而必有a-a²＞0，即0＜a＜1，
进一步，考虑到此时

b

1-a

＞0，
再根据g（

b 1-a

）=

b

1-a

(2-2a-b)≥0，
得2a+b≤2，
所以，a，b满足和必要条件为0＜b≤1，0＜a＜1，2a+b≤2．③
下面证明，对满足③的任意实数对（a，b）以及任意的实数x，y，
总有①成立，
即对任意x，y取非负值，
事实上，在③成立时，有a（1-b）≥0，a-a²＞0，

b

1-a

(2-2a-b)≥0，
再结合x²+y²≥-2xy，
得h（x，y）≥（a-a²）x²y²+a（1-b）（-2xy）+2axy+（2b-b²）
=（a-a²）x²y²+2abxy+（2b-b²）
=（a-a²）（xy+

b

1-a

）²+

b

1-a

（2-2a-b）≥0．
综上所述，所求的正实数对（a，b）全体为：
{（a，b）|

0＜b≤1 0＜a＜1 2a+b≤2

}，
作出可行域，得点P（a，b）所在区域为梯形OABC，
由OA=1，BC=

1

2

，OC=1，
得点P（a，b）所在区域的面积为：
S=

1

2

(1+

1

2

)×1=

3

4

．

点评：本题考查点所在区域的面积的求法，综合性强，难度大，对数学思维能力的要求较高，解题时要注意等价转化思想和线性规划知识的合理运用．