题目内容
过O极点引直线交圆ρ2+r2-2rρcosθ-a2=0（r＞a＞0）于P，Q两点，在此直线上取一点R，使得
=
+
，求R点的轨迹的极坐标方程（r，a是常数）．
| 2 |
| OR |
| 1 |
| OP |
| 1 |
| OQ |
考点：简单曲线的极坐标方程
专题：坐标系和参数方程
分析：把圆的极坐标方程化为直角坐标方程，设出直线的直角坐标方程，代入圆的方程，利用韦达定理及条件求得 xR=
，再把它化为极坐标方程．
| r2-a2 |
| r |
解答：
解：圆ρ2+r2-2rρcosθ-a2=0（r＞a＞0）化为直角坐标方程为 （x-r）2+y2=a2，
表示以（r，0）为圆心、半径等于a的圆．
设直线的直角坐标方程设为y=kx，代入圆的方程化简可得 （k2+1）x2-2rx+r2-a2=0，
利用韦达定理可得 xP+xQ=
，xP•xQ=
．
再根据
=
+
，可得
=
+
=
=
，
求得 xR=
，再化为极坐标方程为 ρcosθ=
．
表示以（r，0）为圆心、半径等于a的圆．
设直线的直角坐标方程设为y=kx，代入圆的方程化简可得 （k2+1）x2-2rx+r2-a2=0，
利用韦达定理可得 xP+xQ=
| 2r |
| k2+1 |
| r2-a2 |
| k2+1 |
再根据
| 2 |
| OR |
| 1 |
| OP |
| 1 |
| OQ |
| 2 |
| xR |
| 1 |
| xP |
| 1 |
| xQ |
| xP+xQ |
| xP•xQ |
| 2r |
| r2-a2 |
求得 xR=
| r2-a2 |
| r |
| r2-a2 |
| r |
点评：本题主要考查点的极坐标与直角坐标的互化，一元二次方程根与系数的关系，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
已知集合S={x||x-1|≤2，x∈R}，T={x|
≥0，x∈Z}，则S∩T=（ ）
| 5 |
| x+1 |
| A、{x|0＜x＜3，x∈Z} |
| B、{x|0≤x≤3，x∈Z} |
| C、{x|-1≤x≤3，x∈Z} |
| D、{x|-1＜x＜3，x∈Z} |
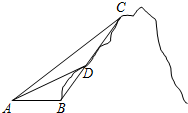某旅游景点有一座风景秀丽的山峰，游客可以乘长为3km的索道AC上山，也可以沿山路BC上山，山路BC中间有一个距离山脚B为1km的休息点D．已知∠ABC=120°，∠ADC=150°．假设小王和小李徒步攀登的速度为每小时1.2km，请问：两位登山爱好者能否在2个小时内徒步登上山峰（即从B点出发到达C点）