题目内容
20.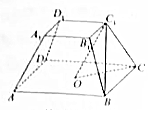 如图,正四棱台ABCD-A1B1C1D1的高为2,下底面中心为O,上、下底面边长分别为2和4.
如图,正四棱台ABCD-A1B1C1D1的高为2,下底面中心为O,上、下底面边长分别为2和4.(1)证明:直线OC1∥平面ADD1A1;
(2)求二面角B-CC1-O的余弦值.
分析 (1)法一:推导出四边形AOC1A1是平行四边形,从而AA1∥OC1,由此能证明直线OC1∥平面ADD1A1.
法二:设上底面中心为O1,以O为原点,OA为x轴,OB为y轴,OO1为z轴,建立空间直角坐标系,利用向量法能证明直线OC1∥平面ADD1A1.
(2)求出平面BCC1的法向量和平面CC1O的法向量,利用向量法能求出二面角B-CC1-O的余弦值.
解答 证明:(1)证法一:∵正四棱台ABCD-A1B1C1D1的高为2,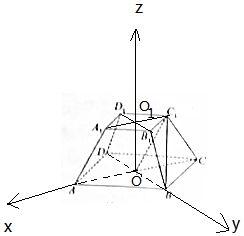
下底面中心为O,上、下底面边长分别为2和4.
∴AO$\underset{∥}{=}$A1C1,∴四边形AOC1A1是平行四边形,
∴AA1∥OC1,
∵AA1?平面ADD1A1,OC1?平面ADD1A1,
∴直线OC1∥平面ADD1A1.
证法二:设上底面中心为O1,以O为原点,OA为x轴,OB为y轴,OO1为z轴,
建立空间直角坐标系,
O(0,0,0),C1(-$\sqrt{2}$,0,2),A(2$\sqrt{2}$,0,0),
D(-$\sqrt{2}$,0,2),A1($\sqrt{2},0,2$),
$\overrightarrow{O{C}_{1}}$=(0,-$\sqrt{2}$,2),$\overrightarrow{AD}$=(-2$\sqrt{2}$,-$\sqrt{2}$,0),$\overrightarrow{A{A}_{1}}$=(-$\sqrt{2}$,0,2),
设平面ADD1A1的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AD}=-2\sqrt{2}x-\sqrt{2}y=0}\\{\overrightarrow{n}•\overrightarrow{A{A}_{1}}=-\sqrt{2}x+2z=0}\end{array}\right.$,取x=$\sqrt{2}$,得$\overrightarrow{n}$=($\sqrt{2}$,-2$\sqrt{2}$,1),
$\overrightarrow{O{C}_{1}}$$•\overrightarrow{n}$=-2+2=0.
∵OC1?平面ADD1A1,
∴直线OC1∥平面ADD1A1.
解:(2)B(0,$\sqrt{2}$,0),C(-2$\sqrt{2}$,0,0),
$\overrightarrow{BC}$=(-2$\sqrt{2}$,-$\sqrt{2}$,0),$\overrightarrow{B{C}_{1}}$=(-$\sqrt{2},-\sqrt{2}$,2),
设平面BCC1的法向量$\overrightarrow{m}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{BC}=-2\sqrt{2}x-\sqrt{2}y=0}\\{\overrightarrow{m}•\overrightarrow{B{C}_{1}}=-\sqrt{2}x-\sqrt{2}y+2z=0}\end{array}\right.$,取x=1,得$\overrightarrow{m}$=(1,-2,-$\frac{\sqrt{2}}{2}$),
平面CC1O的法向量$\overrightarrow{p}$=(1,0,0),
设二面角B-CC1-O的平面角为θ,
则cosθ=$\frac{|\overrightarrow{m}•\overrightarrow{p}|}{|\overrightarrow{m}|•|\overrightarrow{p}|}$=$\frac{1}{\sqrt{1+4+\frac{1}{2}}}$=$\frac{2\sqrt{11}}{11}$.
∴二面角B-CC1-O的余弦值为$\frac{2\sqrt{11}}{11}$.
点评 本题考查线面平行的证明,考查二面角的余弦值的求法,是中档题,注意向量法的合理运用.

| A. | (-$\frac{3}{2}$,$\frac{5}{2}$) | B. | ($\frac{3}{2}$,$\frac{5}{2}$) | C. | (-$\frac{5}{2}$,$\frac{7}{2}$) | D. | ($\frac{5}{2}$,$\frac{7}{2}$) |
 中国诗词大会节目是央视首档全民参与的诗词节目,节目以“赏中华诗词、寻文化基因、品生活之美”为基本宗旨,力求通过对诗词知识的比拼及赏析,带动全民重温那些曾经学过的古诗词,分享诗词之美,感受诗词之趣,从古人的智慧和情怀中汲取营养,涵养心灵.如图是2016年中国诗词大会中,七位评委为甲、乙两名选手打出的分数的茎叶图(其中m为数字0~9中的一个),去掉一个最高分和一个最低分后,甲、乙两名选手得分的平均数分别为a1,a2,则一定有( )
中国诗词大会节目是央视首档全民参与的诗词节目,节目以“赏中华诗词、寻文化基因、品生活之美”为基本宗旨,力求通过对诗词知识的比拼及赏析,带动全民重温那些曾经学过的古诗词,分享诗词之美,感受诗词之趣,从古人的智慧和情怀中汲取营养,涵养心灵.如图是2016年中国诗词大会中,七位评委为甲、乙两名选手打出的分数的茎叶图(其中m为数字0~9中的一个),去掉一个最高分和一个最低分后,甲、乙两名选手得分的平均数分别为a1,a2,则一定有( )| A. | a1>a2 | B. | a2>a1 | ||
| C. | a1=a2 | D. | a1,a2的大小与m的值有关 |
| A. | [-3,1] | B. | [-4,2] | C. | [-2,1] | D. | (-3,1] |
| A. | ①② | B. | ①③ | C. | ②③ | D. | ①④ |
| A. | $\frac{1}{4},\frac{1}{4},\frac{1}{2}$ | B. | $\frac{1}{4},\frac{1}{4},\frac{1}{4}$ | C. | $\frac{1}{3},\frac{1}{3},\frac{1}{2}$ | D. | $\frac{1}{4},\frac{1}{3},\frac{1}{2}$ |




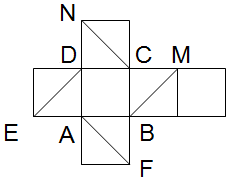 如图是正方体的平面展开图,则下列结论中正确的有(3)(4).
如图是正方体的平面展开图,则下列结论中正确的有(3)(4).