题目内容
15.若$\frac{1}{a}$>$\frac{1}{b}$>0,有四个不等式:①a3<b3;②loga+23>logb+13;③④$\sqrt{b}$-$\sqrt{a}$<$\sqrt{b-a}$;④a3+b3>2ab2,则下列组合中全部正确的为( )| A. | ①② | B. | ①③ | C. | ②③ | D. | ①④ |
分析 根据不等式的性质分别对①②③④判断即可.
解答 解:若$\frac{1}{a}$>$\frac{1}{b}$>0,则b>a>0,
①a3<b3,正确;
②令b=2,a=1,则loga+23=logb+13;故②错误;
③由$\sqrt{b}$-$\sqrt{a}$<$\sqrt{b-a}$,
得:b+a-2$\sqrt{ab}$<b-a,
故a<$\sqrt{ab}$,故a<b,成立,
故③正确;
④∵b>a>0,∴a2-2ab+b2>0,∴a2-ab+b2>ab(*).
而a,b均为正数,∴a+b>0,
∴(a+b)(a2-ab+b2)>ab(a+b),
∴a3+b3>a2b+ab2 成立.
而2ab2>a2b+ab2,故④不一定成立,故④错误;
故选:B.
点评 本题主要考查用分析法和综合法证明不等式,此题还可用比较法证明,体会不同方法间的区别联系,属于中档题.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
3.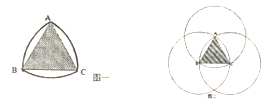 如图一所示,由弧AB,弧AC,弧BC所组成的图形叫做勒洛三角形,它由德国机械工程专家、机械运动学家勒洛首先发现的,它的构成如图二所示,以正三角形ABCd的每个顶点为圆心,以边长为半径,在另两个顶点间作一段弧,由三段弧所围成的曲边三角形即为勒洛三角形,有一个如图一所示的靶子,某人向靶子射出一箭,若此箭一定能射中靶子且射中靶子中的任意一点是等可能的,则此箭恰好射中三角形ABC内部(即阴影部分)的概率为( )
如图一所示,由弧AB,弧AC,弧BC所组成的图形叫做勒洛三角形,它由德国机械工程专家、机械运动学家勒洛首先发现的,它的构成如图二所示,以正三角形ABCd的每个顶点为圆心,以边长为半径,在另两个顶点间作一段弧,由三段弧所围成的曲边三角形即为勒洛三角形,有一个如图一所示的靶子,某人向靶子射出一箭,若此箭一定能射中靶子且射中靶子中的任意一点是等可能的,则此箭恰好射中三角形ABC内部(即阴影部分)的概率为( )
 如图一所示,由弧AB,弧AC,弧BC所组成的图形叫做勒洛三角形,它由德国机械工程专家、机械运动学家勒洛首先发现的,它的构成如图二所示,以正三角形ABCd的每个顶点为圆心,以边长为半径,在另两个顶点间作一段弧,由三段弧所围成的曲边三角形即为勒洛三角形,有一个如图一所示的靶子,某人向靶子射出一箭,若此箭一定能射中靶子且射中靶子中的任意一点是等可能的,则此箭恰好射中三角形ABC内部(即阴影部分)的概率为( )
如图一所示,由弧AB,弧AC,弧BC所组成的图形叫做勒洛三角形,它由德国机械工程专家、机械运动学家勒洛首先发现的,它的构成如图二所示,以正三角形ABCd的每个顶点为圆心,以边长为半径,在另两个顶点间作一段弧,由三段弧所围成的曲边三角形即为勒洛三角形,有一个如图一所示的靶子,某人向靶子射出一箭,若此箭一定能射中靶子且射中靶子中的任意一点是等可能的,则此箭恰好射中三角形ABC内部(即阴影部分)的概率为( )| A. | $\frac{\sqrt{3}}{2π-\sqrt{3}}$ | B. | $\frac{\sqrt{3}}{2(π-\sqrt{3}})$ | C. | $\frac{2π-3\sqrt{3}}{2(π-\sqrt{3})}$ | D. | $\frac{2π-2\sqrt{3}}{2π-\sqrt{3}}$ |
2.用秦九韶算法计算多项式f(x)=3x6+5x5+6x4+79x3-8x2+35x+12在x=-4时的值时,运算总次数为( )
| A. | 11 | B. | 12 | C. | 26 | D. | 27 |
 已知椭圆C;$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>c)的左、右焦点分别为F1(-c,0)、F2(c,0),过原点O的直线(与x轴不重合)与椭圆C相交于D、Q两点,且|DF1|+|QF1|=4,P为椭圆C上的动点,△PF1F2的面积的最大值为$\sqrt{3}$.
已知椭圆C;$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>c)的左、右焦点分别为F1(-c,0)、F2(c,0),过原点O的直线(与x轴不重合)与椭圆C相交于D、Q两点,且|DF1|+|QF1|=4,P为椭圆C上的动点,△PF1F2的面积的最大值为$\sqrt{3}$.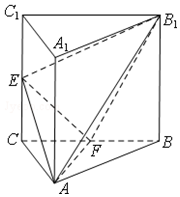 如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,△ABC为等腰直角三角形,∠BAC=90°,且AA1=AB=2,E,F分别是CC1,BC的中点.
如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,△ABC为等腰直角三角形,∠BAC=90°,且AA1=AB=2,E,F分别是CC1,BC的中点.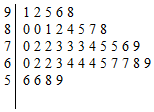 中国诗词大会的播出引发了全民的读书热,某小学语文老师在班里开展了一次诗词默写比赛,班里40名学生得分数据的茎叶图如图所示.若规定得分不小于85分的学生得到“诗词达人”的称号,小于85分且不小于70分的学生得到“诗词能手”的称号,其他学生得到“诗词爱好者”的称号,根据该次比赛的成就按照称号的不同进行分层抽样抽选10名学生,则抽选的学生中获得“诗词能手”称号的人数为( )
中国诗词大会的播出引发了全民的读书热,某小学语文老师在班里开展了一次诗词默写比赛,班里40名学生得分数据的茎叶图如图所示.若规定得分不小于85分的学生得到“诗词达人”的称号,小于85分且不小于70分的学生得到“诗词能手”的称号,其他学生得到“诗词爱好者”的称号,根据该次比赛的成就按照称号的不同进行分层抽样抽选10名学生,则抽选的学生中获得“诗词能手”称号的人数为( )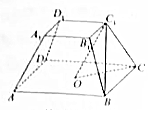 如图,正四棱台ABCD-A1B1C1D1的高为2,下底面中心为O,上、下底面边长分别为2和4.
如图,正四棱台ABCD-A1B1C1D1的高为2,下底面中心为O,上、下底面边长分别为2和4.