题目内容
2.若椭圆$\frac{x^2}{4}+\frac{y^2}{m}=1$的离心率$e=\frac{{\sqrt{3}}}{2}$,则实数m的值是( )| A. | 1 | B. | 1或16 | C. | $\frac{4}{3}$ | D. | 16 |
分析 根据题意,根据椭圆的焦点位置不同分2种情况讨论,①、椭圆的焦点在x轴上,②、椭圆的焦点在y轴上;每种情况下由标准方程求出a、b的值,结合a、b、c的关系求出c的值,进而由离心率公式可得关于m的方程,解可得m的值,综合两种情况即可得答案.
解答 解:根据题意,椭圆的方程为$\frac{x^2}{4}+\frac{y^2}{m}=1$,分2种情况讨论:
①、椭圆的焦点在x轴上,有a=$\sqrt{4}$=2,b=$\sqrt{m}$,
则c=$\sqrt{4-m}$,
其离心率e=$\frac{c}{a}$=$\frac{\sqrt{4-m}}{2}$=$\frac{\sqrt{3}}{2}$,
解可得m=1,
②、椭圆的焦点在y轴上,有b=$\sqrt{4}$=2,a=$\sqrt{m}$,
则c=$\sqrt{m-4}$,
其离心率e=$\frac{c}{a}$=$\frac{\sqrt{m-4}}{\sqrt{m}}$=$\frac{\sqrt{3}}{2}$,
解可得m=16,
综合可得m=1或16;
故选:B.
点评 本题考查椭圆的性质,注意需要对椭圆的焦点的位置进行分类讨论,这是本题的易错点.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
13.若A点坐标为(1,1),F1是椭圆5x2+9y2=45的左焦点,点P是该椭圆上的动点,则|PA|+|PF1|的最大值为( )
| A. | $6-\sqrt{2}$ | B. | $6+\sqrt{2}$ | C. | $5+\sqrt{2}$ | D. | $7+\sqrt{2}$ |
14.函数y=f(x)的图象如图,则( )
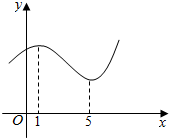

| A. | f′(3)>3 | B. | f′(3)<3 | C. | f′(3)=3 | D. | f′(3)的符号不确定 |
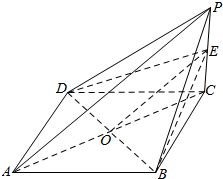 如图所示,在四棱锥P-ABCD中,四边形ABCD是边长为2的正方形,平面ABCD⊥平面PCD,∠PCD=90°,PC=1.5,E是侧棱PC上的动点.
如图所示,在四棱锥P-ABCD中,四边形ABCD是边长为2的正方形,平面ABCD⊥平面PCD,∠PCD=90°,PC=1.5,E是侧棱PC上的动点.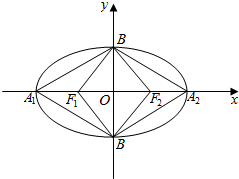 如图所示,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),A1、A2、B1、B2、F1、F2分别是其左右顶点,上下顶点和左右焦点,四边形A1B1A2B2的面积是四边形B1F2B2F1面积的2倍.
如图所示,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),A1、A2、B1、B2、F1、F2分别是其左右顶点,上下顶点和左右焦点,四边形A1B1A2B2的面积是四边形B1F2B2F1面积的2倍.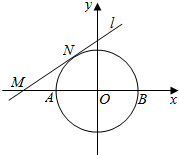 已知圆O:x2+y2=1与x轴交于A,B两点,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率是$\frac{\sqrt{2}}{2}$,且与圆O恰有两个公共点.
已知圆O:x2+y2=1与x轴交于A,B两点,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率是$\frac{\sqrt{2}}{2}$,且与圆O恰有两个公共点.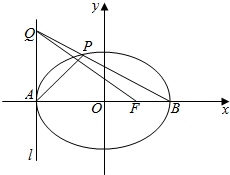 如图,A、B分别是椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{{b}^{2}}$=1(2>b>0)的左右顶点,F为其右焦点,|AF|×|FB|=3.
如图,A、B分别是椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{{b}^{2}}$=1(2>b>0)的左右顶点,F为其右焦点,|AF|×|FB|=3.