题目内容
7.△ABC外接圆的半径为$\sqrt{2}$,圆心为O,BC=2,且∠ABC为锐角,则$\overrightarrow{OA}$$•\overrightarrow{BC}$的取值范围是( )| A. | (-2,2$\sqrt{2}$] | B. | (-2$\sqrt{2}$,2] | C. | [-2$\sqrt{2}$,2$\sqrt{2}$] | D. | (-2,2) |
分析 判断$\overrightarrow{OA},\overrightarrow{BC}$的夹角的范围,根据余弦定理得出AB,AC的关系,使用数量积的运算公式利用排除法选出答案.
解答 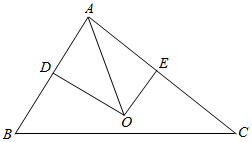 解:过O作OD⊥AB,OE⊥AC,则D,E分别是AB,AC的中点,
解:过O作OD⊥AB,OE⊥AC,则D,E分别是AB,AC的中点,
则$\overrightarrow{OA}•\overrightarrow{BC}$=$\overrightarrow{OA}•(\overrightarrow{BA}+\overrightarrow{AC})$=OA•AB•cos∠BAO-OA•AC•cos∠CAO=AB•AD-AC•AE=$\frac{1}{2}A{B}^{2}-\frac{1}{2}A{C}^{2}$.
∵∠ABC是锐角,
∴cos∠ABC=$\frac{A{B}^{2}+B{C}^{2}-A{C}^{2}}{2AB•BC}$=$\frac{A{B}^{2}-A{C}^{2}+4}{4AB}$>0.
∴AB2-AC2>-4.
∴$\overrightarrow{OA}•\overrightarrow{BC}$=$\frac{1}{2}$(AB2-AC2)>-2.排除B,C.
∵O为△ABC的外接圆圆心,∴$\overrightarrow{OA},\overrightarrow{BC}$的夹角θ不等于0°.
∴$\overrightarrow{OA}•\overrightarrow{BC}$=OA•BC•cosθ=2$\sqrt{2}$cosθ≠2$\sqrt{2}$.排除A.
故选:D.
点评 本题考查了平面向量的数量积运算,向量加法的几何意义,余弦定理,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.某几何体的三视图如图所示,则该几何体外接球的表面积为( )


| A. | 4π | B. | 5π | C. | 6π | D. | 7π |
2.cos60°sin75°+sin60°sin165°的值是( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | 1 |
12.已知实系数一元二次方程x2+(1+a)x+a+b+1=0的两个实根为x1,x2,且 0<x1<1<x2,则$\frac{b}{a}$的取值范围是( )
| A. | (-1,$\frac{1}{2}$) | B. | (-2,$\frac{1}{2}$) | C. | $(-1,-\frac{1}{2})$ | D. | $(-2,-\frac{1}{2})$ |
19.已知直线l的倾斜角为α,斜率为k,则“$α<\frac{π}{3}$”是“$k<\sqrt{3}$”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分也非必要条件 |