题目内容
2．cos60°sin75°+sin60°sin165°的值是（ ）| A． | $\frac{\sqrt{2}}{2}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | $\frac{1}{2}$ | D． | 1 |
分析 直接利用诱导公式以及两角和与差的三角函数化简求解即可．
解答 解：cos60°sin75°+sin60°sin165°
=cos60°cos15°+sin60°sin15°
=cos（60°-15°）
=cos45°
=$\frac{\sqrt{2}}{2}$．
故选：A．
点评 本题考查两角和与差的三角函数，三角函数的化简求值，考查计算能力．
练习册系列答案
轻松暑假总复习系列答案
相关题目
13．投掷一枚质地均匀的骰子两次，记A={两次的点数均为奇数}，B={两次的点数之和为4}，则P（B|A）=（ ）
| A． | $\frac{1}{12}$ | B． | $\frac{1}{4}$ | C． | $\frac{2}{9}$ | D． | $\frac{2}{3}$ |
10．若非零向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow{a}$=2|$\overrightarrow{b}$|=|$\overrightarrow{a}$-3$\overrightarrow{b}$|，则$\overrightarrow{a}$，$\overrightarrow{b}$夹角的余弦值为（ ）
| A． | $-\frac{3}{8}$ | B． | $\frac{3}{8}$ | C． | $-\frac{3}{4}$ | D． | $\frac{3}{4}$ |
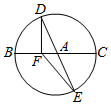如图，BC是半径为3的圆A的一条直径，F是线段AB上的点，且$\overrightarrow{BF}$=2$\overrightarrow{FA}$，若DE是圆A中绕圆心A运动的一条直径，则$\overrightarrow{FD}$•$\overrightarrow{FE}$的值为（ ）
7．△ABC外接圆的半径为$\sqrt{2}$，圆心为O，BC=2，且∠ABC为锐角，则$\overrightarrow{OA}$$•\overrightarrow{BC}$的取值范围是（ ）
| A． | （-2，2$\sqrt{2}$] | B． | （-2$\sqrt{2}$，2] | C． | [-2$\sqrt{2}$，2$\sqrt{2}$] | D． | （-2，2） |
如图，有一块荒地，形状为一个角，把这个角记为∠A（角的两边足够长），经测量∠A=120°，现在分别在∠A的两边选取P，Q两点，且PQ=200米．