题目内容
给出下列命题:
①函数y=2-|x|为偶函数;
②函数y=1是周期函数;
③函数f(x)=2x-x2的零点有2个;
④函数g(x)=|log2x|-(
)x在(0,+∞)上恰有两个零点x1,x2且x1•x2<1.
其中正确命题的个数是( )
①函数y=2-|x|为偶函数;
②函数y=1是周期函数;
③函数f(x)=2x-x2的零点有2个;
④函数g(x)=|log2x|-(
| 1 |
| 2 |
其中正确命题的个数是( )
| A、1 | B、2 | C、3 | D、4 |
考点:命题的真假判断与应用
专题:函数的性质及应用
分析:由函数的奇偶性的定义,即可判断①;运用函数的周期性,即可判断②;画出y=x2,y=2x的图象,注意f(2)=0,f(4)=0,从而判断③;作出y=|log2x|和y=(
)x在(0,+∞)上的图象,结合图象判断交点个数和范围,即可判断④.
| 1 |
| 2 |
解答:
 解:①函数y=2-|x|为偶函数,由于f(-x)=2-|-x|=2-|x|=f(x),
解:①函数y=2-|x|为偶函数,由于f(-x)=2-|-x|=2-|x|=f(x),
故①正确;
②函数y=1,即f(x)=1,存在非零常数T,有f(x+T)=f(x),
故为周期函数,即②正确;
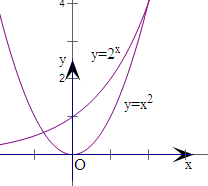
③函数f(x)=2x-x2的零点,即令f(x)=0,2x=x2,
显然有f(2)=0,f(4)=0,当x<0时,y=x2递减,
y=2x递增,显然有一个交点,故有三个交点,故③错;
④令g(x)=0,则|log2x|=(
)x,
作出y=|log2x|和y=(
)x在(0,+∞)上的图象,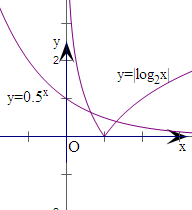
可知恰有两个交点,设零点为x1,x2且
|log2x1|>|log2x2|,x1<1,x2>1,
故有
>x2,即x1x2<1,故④正确.
故选C.
 解:①函数y=2-|x|为偶函数,由于f(-x)=2-|-x|=2-|x|=f(x),
解:①函数y=2-|x|为偶函数,由于f(-x)=2-|-x|=2-|x|=f(x),故①正确;
②函数y=1,即f(x)=1,存在非零常数T,有f(x+T)=f(x),
故为周期函数,即②正确;
③函数f(x)=2x-x2的零点,即令f(x)=0,2x=x2,
显然有f(2)=0,f(4)=0,当x<0时,y=x2递减,
y=2x递增,显然有一个交点,故有三个交点,故③错;
④令g(x)=0,则|log2x|=(
| 1 |
| 2 |
作出y=|log2x|和y=(
| 1 |
| 2 |
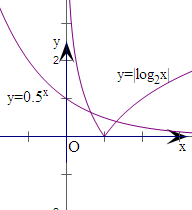
可知恰有两个交点,设零点为x1,x2且
|log2x1|>|log2x2|,x1<1,x2>1,
故有
| 1 |
| x1 |
故选C.
点评:本题主要考查函数的奇偶性和周期性及运用,考查函数的零点个数的判断,掌握运用图象求交点个数,注意运用数形结合思想,是一道中档题.

练习册系列答案
相关题目
阅读如图所示程序,则输出的s的值是( )


| A、17 | B、19 | C、21 | D、23 |
函数f(x)=ax+logax在[1,2]上的最大值和最小值之差为|a2-a|+1,则a值为( )
A、2或
| ||
| B、2或4 | ||
C、
| ||
| D、2 |
 如图所示,AB为⊙O直径,CD切⊙O于D,AB延长线交CD于点C,若∠CAD=25°,则∠C为( )
如图所示,AB为⊙O直径,CD切⊙O于D,AB延长线交CD于点C,若∠CAD=25°,则∠C为( )| A、45° | B、40° |
| C、35° | D、30° |
下列各函数值,其中符号为负的是( )
| A、sin(-1000°) | ||||||
| B、cos(-2200°) | ||||||
| C、tan(-10) | ||||||
D、
|
在一个三角形的三边长之比为3:5:7,则其最大的角是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
若函数f(x)在x0处可导,
的值为( )
| lim |
| x→x0 |
| f(x0)-f(x) |
| x-x0 |
| A、f′(x0) |
| B、-f′(x0) |
| C、f′(x) |
| D、-f′(x) |
 如图,四棱锥A-BCDE中,底面BCDE为矩形,侧面ABC⊥底面BCDE,BC=2,CD=
如图,四棱锥A-BCDE中,底面BCDE为矩形,侧面ABC⊥底面BCDE,BC=2,CD=