题目内容
3.已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+y2=1(1<a<4)的右顶点到直线x=4的距离为1,则椭圆的离心率为( )| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\frac{2\sqrt{2}}{3}$ |
分析 由题意知|a-4|=1,从而解得a=3,c=$\sqrt{9-1}$=2$\sqrt{2}$,从而求得.
解答 解:椭圆$\frac{{x}^{2}}{{a}^{2}}$+y2=1的右项点为(a,0),
故|a-4|=1,
解得,a=3或a=5(舍去),
故c=$\sqrt{9-1}$=2$\sqrt{2}$,
故椭圆的离心率为e=$\frac{c}{a}$=$\frac{2\sqrt{2}}{3}$,
故选:D.
点评 本题考查了椭圆的标准方程与椭圆的几何性质的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.正方体ABCD-A1B1C1D1的棱长为a,E,F分别是BB1,CD的中点,则点F到平面A1D1E的距离为( )
| A. | $\frac{3}{10}$a | B. | $\frac{3\sqrt{7}}{10}$a | C. | $\frac{3\sqrt{5}}{10}$a | D. | $\frac{7}{10}$a |
14.设双曲线$\frac{{y}^{2}}{4}$-x2=1上的点P到点(0,$\sqrt{5}$)的距离为6,则P点到(0,-$\sqrt{5}$)的距离是( )
| A. | 2或10 | B. | 10 | C. | 2 | D. | 4或8 |
18.函数满足f(x+1)=xf(x),且当x∈[0,1)时,f(x)=x2,若在区间(-1,1)上,g(x)=f(x)-mx+1有两个零点,则m的范围( )
| A. | m<-$\frac{5}{4}$或m>2 | B. | m>2 | C. | -$\frac{5}{4}$<m≤-1或m=2 | D. | -$\frac{5}{4}$<m≤-1或m>2 |
8.如图,网格纸上小正方形边长为1,粗线是一个棱锥的三视图,则此棱锥与外接球的体积比为( )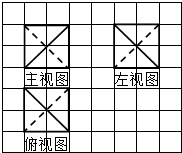

| A. | $\frac{2\sqrt{3}}{9π}$ | B. | $\frac{\sqrt{3}}{9π}$ | C. | $\frac{\sqrt{2}}{16π}$ | D. | $\frac{8\sqrt{2}}{π}$ |
15.函数f(x)=5sin($\frac{x}{3}$-$\frac{π}{10}$)(x∈R)的最大值和最小正周期分别是( )
| A. | 5,2π | B. | 1,6π | C. | 1,2π | D. | 5,6π |
13.已知O(0,0,0),A(1,2,3),B(2,1,2),P(1,1,2),点Q在直线OP上运动,当$\overrightarrow{QA}$•$\overrightarrow{QB}$取最小值时,点Q的坐标是( )
| A. | ($\frac{4}{3}$,$\frac{4}{3}$,$\frac{8}{3}$) | B. | (-$\frac{4}{3}$,-$\frac{4}{3}$,$\frac{8}{3}$) | C. | ($\frac{4}{3}$,$\frac{4}{3}$,-$\frac{8}{3}$) | D. | (-$\frac{4}{3}$,-$\frac{4}{3}$,-$\frac{8}{3}$) |