题目内容
已知sin(
+θ)+2(sin
-θ)=0,则tan(
+θ)= .
| 12π |
| 5 |
| 11π |
| 10 |
| 2π |
| 5 |
考点:两角和与差的正切函数,同角三角函数基本关系的运用,运用诱导公式化简求值
专题:计算题,三角函数的求值
分析:用诱导公式化简后等式两边同时除以cos
cosθ,再根据两角和与差的正切函数公式化简即可求值.
| 2π |
| 5 |
解答:
解:sin(
+θ)+2×(sin
-θ)=0,
⇒sin
cosθ+cos
sinθ+2×(sin
cosθ-cos
sinθ)=0
⇒sin
cosθ+cos
sinθ+2×(-cos
cosθ+sin
sinθ)=0
等式两边同时除以cos
cosθ,
⇒tan
+tanθ+2(tan
tanθ-1)=0
⇒
=2
⇒tan(
+θ)=2
故答案为:2.
| 12π |
| 5 |
| 11π |
| 10 |
⇒sin
| 2π |
| 5 |
| 2π |
| 5 |
| 11π |
| 10 |
| 11π |
| 10 |
⇒sin
| 2π |
| 5 |
| 2π |
| 5 |
| 2π |
| 5 |
| 2π |
| 5 |
等式两边同时除以cos
| 2π |
| 5 |
⇒tan
| 2π |
| 5 |
| 2π |
| 5 |
⇒
tan
| ||
1-tan
|
⇒tan(
| 2π |
| 5 |
故答案为:2.
点评:本题主要考查了两角和与差的正切函数公式的应用,运用诱导公式化简求值,同角三角函数基本关系的运用,属于基本知识的考查.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
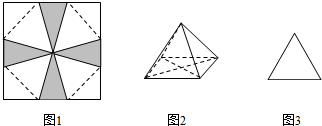
将一张边长为6cm的纸片按如图1所示的阴影部分截去四个全等的等腰三角形,将剩余下部分沿虚线折叠并拼成一个有底的正四棱锥(底面是正方形,顶点在底面的射影为正方形的中心)模型,如图2放置,若正四棱锥的正视图是正三角形(如图3),则正四棱锥的体积是( )

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在正方体ABCD-A1B1C1D1中,M是BC的中点,点P是面DCC1D1所在的平面内的动点,且满足∠APD=∠MPC,则点P的轨迹是( )
| A、圆 | B、椭圆 | C、双曲线 | D、抛物线 |
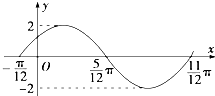 函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|φ|<
函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|φ|<