题目内容
13.已知命题p:关于x的方程x2-ax+4=0有实根;命题q:关于x的函数y=2x2+ax+4在[3,+∞)上是增函数,若p∧q是真命题,则实数a的取值范围是[-12,-4]∪[4,+∞).分析 根据条件求出命题p,q为真命题的等价条件,结合复合命题真假关系进行求解即可.
解答 解:命题p:关于x的方程x2-ax+4=0有实根,则△=a2-16≥0,解得a≥4,或a≤-4.
命题q:关于x的函数y=2x2+ax+4在[3,+∞)上是增函数,∴$-\frac{a}{4}≤3$,解得a≥-12.
若p∧q是真命题,
则p,q同时为真命题,
则$\left\{\begin{array}{l}{a≥4或a≤-4}\\{a≥-12}\end{array}\right.$,
即-12≤a≤-4或a≥4,
故答案为:[-12,-4]∪[4,+∞)
点评 本题考查了复合命题真假的判定方法、函数的性质、一元二次的实数根与判别式的关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
8.已知实数x,y满足的约束条件$\left\{\begin{array}{l}x-2y+2≥0\\ 3x-2y-3≤0\\ x+y-1≥0\end{array}\right.$,表示的平面区域为D,若存在点P(x,y)∈D,使x2+y2≥m成立,则实数m的最大值为( )
| A. | $\frac{181}{16}$ | B. | 1 | C. | $\frac{9}{13}$ | D. | $\frac{1}{2}$ |
18.有5件不同的商品,其中2件次品,3件正品,从中取出2件,至少有1件次品的概率为( )
| A. | $\frac{4}{5}$ | B. | $\frac{7}{10}$ | C. | $\frac{3}{5}$ | D. | $\frac{1}{2}$ |
2.在区间$[{-\frac{5}{6},\frac{13}{6}}]$上随机取一个数x,则事件“$-1≤{log_{\frac{1}{3}}}({x+1})≤1$”不发生的概率为( )
| A. | $\frac{8}{9}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{9}$ |
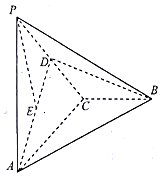 如图,在三棱锥P-ABC中,PA⊥平面ABC,AC⊥BC,D为PC的中点,E为AD的中点,PA=AC=2,BC=1.
如图,在三棱锥P-ABC中,PA⊥平面ABC,AC⊥BC,D为PC的中点,E为AD的中点,PA=AC=2,BC=1. 在斜三棱柱ABC-A1B1C1中,顶点A1在底面ABC内的射影恰为线段AB的中点,AA1=2,△ABC为边长为2的正三角形,N为△ABC的中心,$\overrightarrow{{C}_{1}M}$=2$\overrightarrow{MB}$.
在斜三棱柱ABC-A1B1C1中,顶点A1在底面ABC内的射影恰为线段AB的中点,AA1=2,△ABC为边长为2的正三角形,N为△ABC的中心,$\overrightarrow{{C}_{1}M}$=2$\overrightarrow{MB}$.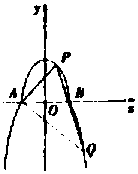 如图,曲线C由上半椭圆${C_1}:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0,y≥0)$和部分抛物线${C_2}:y=-{x^2}+1(y≤0)$连接而成,C1与C2的公共点为A,B,其中C1的离心率为$\frac{{\sqrt{3}}}{2}$.
如图,曲线C由上半椭圆${C_1}:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0,y≥0)$和部分抛物线${C_2}:y=-{x^2}+1(y≤0)$连接而成,C1与C2的公共点为A,B,其中C1的离心率为$\frac{{\sqrt{3}}}{2}$.