题目内容
8.已知实数x,y满足的约束条件$\left\{\begin{array}{l}x-2y+2≥0\\ 3x-2y-3≤0\\ x+y-1≥0\end{array}\right.$,表示的平面区域为D,若存在点P(x,y)∈D,使x2+y2≥m成立,则实数m的最大值为( )| A. | $\frac{181}{16}$ | B. | 1 | C. | $\frac{9}{13}$ | D. | $\frac{1}{2}$ |
分析 作出不等式组对应的平面区域,利用点到直线的距离公式进行转化求解即可.
解答 解:作出不等式组对应的平面区域如图,
x2+y2的几何意义是区域内的点到原点的距离的平方,
由图象知O到直线x+y-1=0的距离最小,
此时d=$\frac{|-1|}{\sqrt{2}}$=$\frac{1}{\sqrt{2}}$,
则d2=$\frac{1}{2}$,
即x2+y2≥$\frac{1}{2}$,
要使x2+y2≥m成立,
则m≤$\frac{1}{2}$,
即实数m的最大值为$\frac{1}{2}$,
故选:D
点评 本题主要考查线性规划的应用,结合点到直线的距离公式求出距离的最小值是解决本题的关键.

练习册系列答案
相关题目
20.已知平面区域D={(x,y)|$\left\{\begin{array}{l}{x-4y+3≤0}\\{3x+5y-25≤0}\\{x≥1}\end{array}\right.$},Z=$\frac{y}{x+2}$.若命题“?(x,y)∈D,Z≥m”为真命题,则实数m的最大值为( )
| A. | $\frac{22}{15}$ | B. | $\frac{2}{7}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
 如图,已知AB为半圆O的直径,点C为半圆上一点,过点C作半圆的切线CD,过点B作BD⊥CD于点D.求证:BC2=BA•BD.
如图,已知AB为半圆O的直径,点C为半圆上一点,过点C作半圆的切线CD,过点B作BD⊥CD于点D.求证:BC2=BA•BD.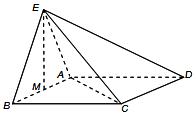 如图,正三角形ABE与菱形ABCD所在的平面互相垂直,AB=2,∠ABC=60°,M是AB的中点.
如图,正三角形ABE与菱形ABCD所在的平面互相垂直,AB=2,∠ABC=60°,M是AB的中点.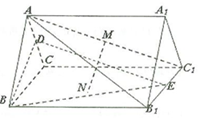 如图,正三棱柱ABC-A1B1C1中,侧棱$A{A_1}=\sqrt{3}$,AB=2,D,E分别为棱AC,B1C1的中点,M,N分别为线段AC1和BE的中点.
如图,正三棱柱ABC-A1B1C1中,侧棱$A{A_1}=\sqrt{3}$,AB=2,D,E分别为棱AC,B1C1的中点,M,N分别为线段AC1和BE的中点.