题目内容
执行如图程序框图.若输入n=20,则输出的S值是( )


A、
| ||
B、
| ||
C、
| ||
D、
|
考点:循环结构
专题:点列、递归数列与数学归纳法,算法和程序框图
分析:模拟执行程序框图,可知该算法的功能是计算并输出数列{
}的求10项和,由裂项法即可求值.
| 1 |
| (2n)2-1 |
解答:
解:模拟执行程序框图,可知该算法的功能是计算并输出数列{
}的求10项和.
S=
+
+
+…+
=
+
+
+…+
=
×(1-
+
-
+…+
-
)
=
.
故选:A.
| 1 |
| (2n)2-1 |
S=
| 1 |
| 22-1 |
| 1 |
| 42-1 |
| 1 |
| 62-1 |
| 1 |
| 202-1 |
=
| 1 |
| 1×3 |
| 1 |
| 3×5 |
| 1 |
| 5×7 |
| 1 |
| 19×20 |
=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 19 |
| 1 |
| 21 |
=
| 10 |
| 21 |
故选:A.
点评:本题主要考察了循环结构和裂项法求数列的前n项和,属于基础题.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
某企业三月中旬生产A、B、C三种产品共3000件,根据分层抽样的结果,企业统计员制作了如下的统计表格.由于不小心,表格中A、C产品的有关数据己被污染看不清楚,统计员记得A产品的样本容量比C产品的样本容量多10件,根据以上信息,可得C产品的数量是( )
| 产品类别 | A | B | C |
| 产品数量(件) | 1300 | ||
| 样本容量(件) | 130 |
| A、900件 | B、800件 |
| C、90件 | D、80件 |
若以点F1(-2,0)、F2(2,0)为焦点的双曲线C过直线l:x+y-1=0上一点M,则能使所作双曲线C的实轴长最长时的双曲线方程为( )
A、x2-
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
双曲线
-
=1上一点P到左焦点F1的距离为9,则P到右焦点F2的距离是( )
| x2 |
| 16 |
| y2 |
| 20 |
| A、1 | B、17 |
| C、1或17 | D、23或41 |
对?x1,x2∈(0,
),若x2>x1,且y1=
,y2=
,则( )
| π |
| 2 |
| 1+sinx1 |
| x1 |
| 1+sinx2 |
| x2 |
| A、y1=y2 |
| B、y1>y2 |
| C、y1<y2 |
| D、y1,y2的大小关系不能确定 |
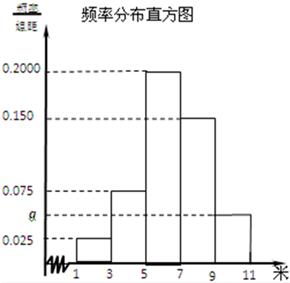 为了解高一年级女生的身体状况,从该高一年级女生中抽取一部分进行“掷铅球”的项目测试,把获得的数据分成[1,3)[3,5)[5,7)[7,9)[9,11)五组(假设测试成绩都不超过11米),画出的频率分布直方图如图所示.已知有4名学生的成绩在9米到11米之间.
为了解高一年级女生的身体状况,从该高一年级女生中抽取一部分进行“掷铅球”的项目测试,把获得的数据分成[1,3)[3,5)[5,7)[7,9)[9,11)五组(假设测试成绩都不超过11米),画出的频率分布直方图如图所示.已知有4名学生的成绩在9米到11米之间.