题目内容
9.已知抛物线C:y2=4x,直线x=ny+4与抛物线C交于A,B两点.(Ⅰ)求证:$\overrightarrow{OA}$•$\overrightarrow{OB}$=0(其中O为坐标原点);
(Ⅱ)设F为抛物线C的焦点,直线l1为抛物线C的准线,直线l2是抛物线C的通径所在的直线,过C上一点P(x0,y0)(y0≠0)作直线l:y0y=2(x+x0)与直线l2相交于点M,与直线l1相交于点N,证明:点P在抛物线C上移动时,$\frac{|MF|}{|NF|}$恒为定值,并求出此定值.
分析 (Ⅰ)直线x=ny+4与抛物线C联立可得y2-4ny-16=0,利用韦达定理及向量的数量积公式即可证明结论;
(Ⅱ)求出M,N的坐标,计算|MF|,|NF|,即可证明结论.
解答 证明:(Ⅰ)设A(x1,y1)、B(x2,y2),
直线x=ny+4与抛物线C联立可得y2-4ny-16=0,
∴y1+y2=4n,y1y2=-16,
∴$\overrightarrow{OA}$•$\overrightarrow{OB}$=x1x2+y1y2=$\frac{{{y}_{1}}^{2}{{y}_{2}}^{2}}{16}$+y1y2=0;
(Ⅱ)证明:将点M,N的横坐标分别代入直线l:y0y=2(x+x0),
得M(1,$\frac{2+2{x}_{0}}{{y}_{0}}$),N(-1,$\frac{-2+2{x}_{0}}{{y}_{0}}$),
∵F(1,0),∴|MF|=|$\frac{2+2{x}_{0}}{{y}_{0}}$|,|NF|=$\sqrt{4+(\frac{-2+2{x}_{0}}{{y}_{0}})^{2}}$=$\frac{2}{|{y}_{0}|}\sqrt{{{y}_{0}}^{2}+({x}_{0}-1)^{2}}$,
∴$\frac{MF|}{|NF|}$=|$\frac{2+2{x}_{0}}{{y}_{0}}$÷$\frac{2}{|{y}_{0}|}\sqrt{{{y}_{0}}^{2}+({x}_{0}-1)^{2}}$=$\frac{1+{x}_{0}|}{\sqrt{4{x}_{0}+({x}_{0}-1)^{2}}}$=1,
∴点P在抛物线C上移动时,$\frac{|MF|}{|NF|}$恒为定值1.
点评 本题考查直线与抛物线的综合运用,考查韦达定理,向量知识的运用,属于中档题.

| A. | $\left\{{\begin{array}{l}{x={t^2}}\\{y={t^4}}\end{array}}\right.$ | B. | $\left\{{\begin{array}{l}{x=sint}\\{y={{sin}^2}t}\end{array}}\right.$ | C. | $\left\{{\begin{array}{l}{x=\sqrt{t}}\\{y=t}\end{array}}\right.$ | D. | $\left\{{\begin{array}{l}{x=t}\\{y={t^2}}\end{array}}\right.$ |
| A. | 9 | B. | 3 | C. | $\sqrt{109}$ | D. | 3$\sqrt{10}$ |

| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
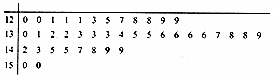 在高三某次数学测试中,40名优秀学生的成绩如图所示:
在高三某次数学测试中,40名优秀学生的成绩如图所示: