题目内容
方程lnx+2x-8=0的实数根的个数是（ ）
| A、0 | B、1 | C、2 | D、3 |
考点：根的存在性及根的个数判断
专题：函数的性质及应用
分析：先将方程变形为：lnx=-2x+8，则原方程的根即为函数y=lnx和函数y=-2x+8图象交点的横坐标，在同一坐标系内做出这两个函数的图象，其交点的个数即为所求．
解答：
解：原方程可化为lnx=-2x+8，则原方程的根即为函数y=lnx和函数y=-2x+8图象交点的横坐标，
在同一坐标系内做出这两个函数的图象：
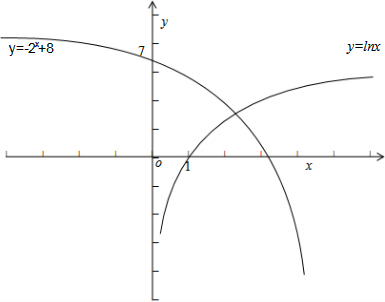
由图象可以看出只有一个交点，所以原方程只有一个实数根．
故答案选B
在同一坐标系内做出这两个函数的图象：
由图象可以看出只有一个交点，所以原方程只有一个实数根．
故答案选B
点评：对于超越方程，方程得确切根没法求出，只能利用图象判断根的个数或根所在的区间，画图时要注意函数图象的特征量（如特征点、特征线等等），属数形结合思想的应用．
练习册系列答案
相关题目
一个平面封闭区域内任意两点距离的最大值称为该区域的“直径”，封闭区域边界曲线的长度与区域直径之比称为区域的“周率”，下面四个平面区域（阴影部分）的周率从左到右依次记为τ1，τ2，τ3，τ4，则下列关系中正确的为（ ）
| A、τ1＞τ4＞τ3 |
| B、τ3＞τ1＞τ2 |
| C、τ4＞τ2＞τ3 |
| D、τ3＞τ4＞τ1 |
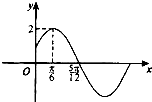已知函数f（x）=2sin（ωx+φ）（ω＞0，|φ|＜| π |
| 2 |
A、f（x）=2sin（
| ||||
B、f（x）=2sin（
| ||||
C、f（x）=2sin（2x-
| ||||
D、f（x）=2sin（2x+
|
若sinα，cosα是方程3x2+6mx+2m+1=0的两根，则实数m的值为（ ）
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
某几何体的三视图如图所示，则该几何体的外接球的球面面积为（ ）
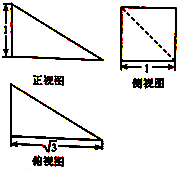
| A、5π | B、12π |
| C、20π | D、8π |
为了解72名学生的学习情况，采用系统抽样的方法，从中抽取容量为8的样本，则分段的间隔为（ ）
| A、9 | B、8 | C、10 | D、7 |
如图，ABCD-A1B1C1D1为正方体，求证：平面A1C1CA⊥平面B1D1DB．