题目内容
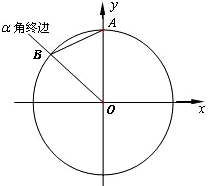如图所示，单位圆（半径为1）的圆心O为坐标原点，它与y轴的正半轴交于点A，与钝角α的终边交于点B（xB，yB），设∠BAO=β，sin2β=| 24 |
| 25 |
考点：三角函数线
专题：三角函数的求值
分析：由题意可得α=
+β，即π-α=
-β．再根据同角三角函数的基本关系求得得sinβ 和cosβ 的值，结合xB =sinβ，yB =cosβ，求得点B（xB，yB）的坐标．
| π |
| 2 |
| π |
| 2 |
解答：
解：由题意可得α=
+β，即π-α=
-β．
再根据sin2β=
=2sinβcosβ，sin2β+cos2β=1，
可得sinβ=
，cosβ=
，或 sinβ=
，cosβ=
．
由于xB =cos（π-α）=cos（
-β）=sinβ，
yB =sin（π-α）=sin（
-β）=cosβ，
故当sinβ=
，cosβ=
时，xB =
，yB =
；
当sinβ=
，cosβ=
时，xB =
，yB=
，
故点B的坐标为（
，
）或（
，
）．
| π |
| 2 |
| π |
| 2 |
再根据sin2β=
| 24 |
| 25 |
可得sinβ=
| 4 |
| 5 |
| 3 |
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
由于xB =cos（π-α）=cos（
| π |
| 2 |
yB =sin（π-α）=sin（
| π |
| 2 |
故当sinβ=
| 4 |
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
当sinβ=
| 3 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
故点B的坐标为（
| 4 |
| 5 |
| 3 |
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
点评：本题主要考查诱导公式，同角三角函数的基本关系，体现了分类讨论、数形结合的数学思想，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
正三棱锥的底面周长为6，侧面都是直角三角形，则此棱锥的体积为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
阅读下边的程序，将输出的X的值依次分别记为x1，x2，x3，…，xn，…设函数f（x）=-2x2+7x-2，对于实数m（0＜m＜3），若f（x）的定义域和值域分别为[m，3]和[1，
]，则m的值为（ ）
| 3 |
| m |
| A、1 | ||
| B、2 | ||
C、
| ||
D、
|
如图，AA1、BB1为圆柱OO1的母线，BC是底面圆O的直径，D，E分别是AA1、CB1的中点，DE⊥面CBB1．