题目内容
若集合A={(x,y)|x2+y2=16},集合B={(x,y)|x2+(y-2)2=a-1},当A∩B=∅时,求实数a的取值范围.
考点:交集及其运算
专题:直线与圆,集合
分析:分a-1<0、a-1=0、a-1>0讨论,当a-1>0时把两集合的交集为∅转化为两圆没有交点求a的范围.
解答:
解:∵x2+y2=16是以(0,0)为圆心,以4为半径的圆,
当a-1<0,即a<1时,B=∅,满足A∩B=∅;
当a-1=0,即a=1时,B={(0,2)},满足A∩B=∅;
当a-1>0时,要满足A∩B=∅,
则
<2,即a<5.
∴A∩B=∅时,实数a的取值范围是(-∞,5).
当a-1<0,即a<1时,B=∅,满足A∩B=∅;
当a-1=0,即a=1时,B={(0,2)},满足A∩B=∅;
当a-1>0时,要满足A∩B=∅,
则
| a-1 |
∴A∩B=∅时,实数a的取值范围是(-∞,5).
点评:本题考查了交集及其运算,考查了两圆间的位置关系,体现了分类讨论的数学思想方法,是基础题.

练习册系列答案
相关题目
某校有教师150人,后勤工作人员20人,高中生1200人,初中生1800人,现要了解该校全体人员对学校的某项规定的看法,抽取一个容量为317的样本进行调查.设计一个合适的抽样方案.你会在初中生中抽取( )人.
| A、120 | B、180 |
| C、200 | D、317 |
过椭圆左焦点F且倾斜角为60°的直线与椭圆交于A、B两点,若
=
,则椭圆的离心率等于( )
| AF |
| 3 |
| 2 |
| FB |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如果
<θ<
,那么下列各式中正确的是( )
| π |
| 4 |
| π |
| 2 |
| A、cosθ<tanθ<sinθ |
| B、sinθ<cosθ<tanθ |
| C、tanθ<sinθ<cosθ |
| D、cosθ<sinθ<tanθ |
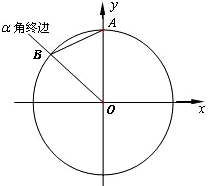 如图所示,单位圆(半径为1)的圆心O为坐标原点,它与y轴的正半轴交于点A,与钝角α的终边交于点B(xB,yB),设∠BAO=β,sin2β=
如图所示,单位圆(半径为1)的圆心O为坐标原点,它与y轴的正半轴交于点A,与钝角α的终边交于点B(xB,yB),设∠BAO=β,sin2β=