题目内容
函数y=（
）|2-x|-m的图象与x轴有交点，则m的取值范围为 ．
| 1 |
| 3 |
考点：指数型复合函数的性质及应用
专题：计算题,函数的性质及应用
分析：函数y=（
）|2-x|-m的图象与x轴有交点可化为方程（
）|2-x|-m=0有解，从而可得m=（
）|2-x|，从而求函数的值域即可．
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
解答：
解：由题意，∵（
）|2-x|-m=0有解，
∴m=（
）|2-x|，
∵|2-x|≥0，
∴0＜（
）|2-x|≤1，
故0＜m≤1，
故答案为：（0，1]．
| 1 |
| 3 |
∴m=（
| 1 |
| 3 |
∵|2-x|≥0，
∴0＜（
| 1 |
| 3 |
故0＜m≤1，
故答案为：（0，1]．
点评：本题考查了函数的图象与函数的零点及方程的根之间的关系，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
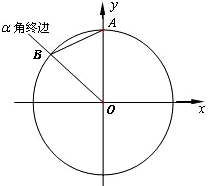如图所示，单位圆（半径为1）的圆心O为坐标原点，它与y轴的正半轴交于点A，与钝角α的终边交于点B（xB，yB），设∠BAO=β，sin2β=已知等差数列{an}的前n项和为Sn，a1+a5=2，且a9=19，则S11=（ ）
| A、260 | B、220 |
| C、130 | D、110 |
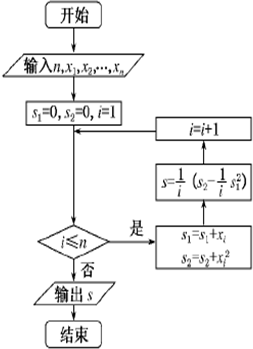某城市缺水问题比较突出，为了制定节水管理办法，对全市居民某年的月均用水量进行了抽样调查，其中n位居民的月均用水量分别为x1，…，xn（单位：吨）．根据如图所示的程序框图，若n=2，且x1，x2分别为1，2，则输出的结果s为函数f（x）=sin（ωx+
）（ω＞0）的最小正周期为π，则该函数图象（ ）
| π |
| 3 |
A、关于直线x=
| ||
B、关于直线x=
| ||
C、关于点（
| ||
D、关于点（
|