题目内容
已知函数y=h(x)的图象与函数y=ax(a>1)的图象关于直线y=x对称,f(x)=h(x+1).
(Ⅰ)求f(x)的解析式;
(Ⅱ)若f(x)在区间[m,n](m>-1)上的值域为[loga
,loga
],求实数p的取值范围;
(Ⅲ)设函数g(x)=loga(x2-3x+3),F(x)=af(x)-g(x),其中a>1.若w≥F(x)对?x∈(-1,+∞)恒成立,求实数w的取值范围.
(Ⅰ)求f(x)的解析式;
(Ⅱ)若f(x)在区间[m,n](m>-1)上的值域为[loga
| p |
| m |
| p |
| n |
(Ⅲ)设函数g(x)=loga(x2-3x+3),F(x)=af(x)-g(x),其中a>1.若w≥F(x)对?x∈(-1,+∞)恒成立,求实数w的取值范围.
考点:指数函数综合题
专题:计算题,函数的性质及应用
分析:(Ⅰ)由已知可得,f(x)=h(x+1)=loga(x+1);
(Ⅱ)由题意可得f(m)=loga(m+1)=loga
,f(n)=loga(n+1)=loga
;从而可得m,n是方程x2+x-p=0在(-1,0)∪(0,+∞)上有两个不同的根,从而解出p;
(Ⅲ)化简F(x)=af(x)-g(x)=
=
,(x>-1);从而化恒成立问题为最值问题.
(Ⅱ)由题意可得f(m)=loga(m+1)=loga
| p |
| m |
| p |
| n |
(Ⅲ)化简F(x)=af(x)-g(x)=
| x+1 |
| x2-3x+3 |
| 1 | ||
(x+1)+
|
解答:
解:(Ⅰ)由已知可得,f(x)=h(x+1)=loga(x+1);
(Ⅱ)∵a>1,
∴f(x)在(-1,+∞)上为增函数,
∴f(m)=loga(m+1)=loga
,
f(n)=loga(n+1)=loga
;
故m+1=
,n+1=
;
则m,n是方程x+1=
的两个不同的根;
即m,n是方程x2+x-p=0在(-1,0)∪(0,+∞)上有两个不同的根;
故
解得,-
<p<0;
(Ⅲ)F(x)=af(x)-g(x)=
=
,(x>-1);
∵(x+1)+
-5≥2
-5;
(当且仅当x=
-1时,等号成立)
∴
∈(0,
],
则若使w≥F(x)对?x∈(-1,+∞)恒成立,
则w≥
.
(Ⅱ)∵a>1,
∴f(x)在(-1,+∞)上为增函数,
∴f(m)=loga(m+1)=loga
| p |
| m |
f(n)=loga(n+1)=loga
| p |
| n |
故m+1=
| p |
| m |
| p |
| n |
则m,n是方程x+1=
| p |
| x |
即m,n是方程x2+x-p=0在(-1,0)∪(0,+∞)上有两个不同的根;
故
|
解得,-
| 1 |
| 4 |
(Ⅲ)F(x)=af(x)-g(x)=
| x+1 |
| x2-3x+3 |
| 1 | ||
(x+1)+
|
∵(x+1)+
| 7 |
| x+1 |
| 7 |
(当且仅当x=
| 7 |
∴
| 1 | ||
(x+1)+
|
2
| ||
| 3 |
则若使w≥F(x)对?x∈(-1,+∞)恒成立,
则w≥
2
| ||
| 3 |
点评:本题考查了函数的性质的应用及基本不等式的应用,同时考查了恒成立问题,属于难题.

练习册系列答案
相关题目
若函数y=f(x)唯一的一个零点同时在区间(0,2),(1,2),(0,4),则下列命题中正确的是( )
| A、函数f(x)在区间(0,1)内有零点 |
| B、函数f(x)在区间(1,1.5)内有零点 |
| C、函数f(x)在区间(2,4)内无零点 |
| D、函数f(x)在区间(1,4)内无零点 |
若x,y满足约束条件
,则z=2x-y的最小值为( )
|
| A、2 | B、4 | C、-2 | D、-4 |
程序框图如图所示,则输出S的值为( )


| A、15 | B、21 | C、22 | D、28 |
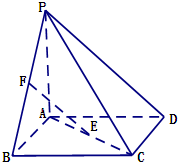 如图,四棱P-ABCD的底面ABCD为正方形,PA⊥底面ABCD,E、F分别是AC、PB的中点.
如图,四棱P-ABCD的底面ABCD为正方形,PA⊥底面ABCD,E、F分别是AC、PB的中点.