题目内容

已知P是椭圆
x2
100
+
y2
36
=1上一点，F1、F2分别是椭圆的左、右焦点，若∠F1PF2=60°，则△PF1F2的面积为
 
．
考点：椭圆的简单性质
专题：圆锥曲线的定义、性质与方程
分析：依题意，在△F1PF2中，∠F1PF2=60°，|F1P|+|PF2|=2a=20，|F1F2|=16，利用余弦定理可求得|F1P|•|PF2|的值，从而可求得△PF1F2的面积．
解答： 解：∵椭圆的方程为
x2
100
+
y2
36
=1，
∴a=10，b=6，c=8．
又∵P为椭圆上一点，∠F1PF2=60°，F1、F2为左右焦点，
∴|F1P|+|PF2|=2a=20，|F1F2|=16，
∴|F1F2|2=（|PF1|+|PF2|）2-2|F1P||PF2|-2|F1P|•|PF2|cos60°
=400-3|F1P|•|PF2|
=256，
∴|F1P|•|PF2|=48．
∴S△PF1F2=
1
2
|F1P|•|PF2|sin60°
=
1
2
×48×
3
2
=12
3
．
故答案为：12
3
．
点评：本题考查椭圆的简单性质，考查余弦定理的应用与三角形的面积公式，属于中档题．
练习册系列答案
相关题目
以椭圆的一个焦点F为圆心作一个圆，使该圆过椭圆的中心O并且与椭圆交于M，N两点，如果|MF|=|MO|，求椭圆的离心率．
已知函数f（x）=（sinx+cosx）2-2
3
cos2x+
3
．
（1）将f（x）的图象向左平移m（m＞0）个单位后，得到偶函数g（x）的图象，求m的最小值；
（2）在区间[0，π]上，求满足f（x）≤2的x的取值集合M．
三棱柱ABC-A1B1C1中，底面边长和侧棱长都相等，∠BAA1=∠CAA1=60°，求证四边形B1BCC1为正方形．
已知函数f'（x）=
2ax2+x-(2a-1)
x2
=
(x+1)[2ax-(2a-1)]
x2
．
（1）若函数f（x）在（0，+∞），f'（x）≥0处取得极值，求f'（x）≤0，（0，+∞）的值；
（2）若a=0，函数f'（x）=
x+1
x2
＞0在f（x）上是单调函数，求（0，+∞）的取值范围．
下列命题：
①
a
•
b
＞0是
a
•
b
的夹角为锐角的充要条件；
②若f（x）在R上满足f（x-2）=-f（x），则f（x）是以4为周期的周期函数；
③函数f（x）=
(
1
2
)x-1，x≤0
log2x，x＞0
，则f（f（
1
2
））的值是1；
④方程lnx+x=4有且仅有一个实数根．
其中正确命题的序号是
 
．（写出所有真命题的代号）
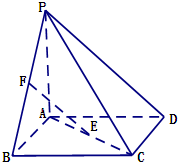如图，四棱P-ABCD的底面ABCD为正方形，PA⊥底面ABCD，E、F分别是AC、PB的中点．
（1）求证：EF∥平面PCD；
（2）求证：平面PBD⊥平面PAC．
已知正项数列{an}，a1=
1
2
，且an+1=
2an
an+2
（*）
（1）求证：{
1
an
}是等差数列，并求{an}的通项公式；
（2）数列{bn}满足bn=e
1
an
，若
mb1b2…bm
（m∈N，m≥2），仍是{bn}中的项，求m在区间[2，2006]中的所有可能值之和S；
（3）若将上述递推关系（*）改为：an+1＜
2an
an+2
，且数列{nan}中任意项nan＜p，试求满足要求的实数p的取值范围．
已知向量
a
=(sinx，
3
2
)，
b
=(
1
2
，cosx)，f（x）=
a
•
b
．
（1）求函数y=f（x）的解析式；
（2）求函数y=f（x）的单调递增区间．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网