题目内容
设函数f(x)=x|x-a|+b,a,b∈R
(1)若a=1,b=-
,求函数f(x)的零点;
(2)若函数f(x)在[0,1]上存在零点,求实数b的取值范围.
(1)若a=1,b=-
| 1 |
| 4 |
(2)若函数f(x)在[0,1]上存在零点,求实数b的取值范围.
考点:函数零点的判定定理
专题:计算题,函数的性质及应用
分析:(1)由题意得,x|x-1|-
=0,讨论去绝对值号求解即可;
(2)函数f(x)在[0,1]上存在零点,即x|x-a|=-b在[0,1]上有解,令g(x)=x|x-a|,只需-b∈{y|y=g(x),x∈[0,1]};故讨论g(x)=x|x-a|的值域即可.
| 1 |
| 4 |
(2)函数f(x)在[0,1]上存在零点,即x|x-a|=-b在[0,1]上有解,令g(x)=x|x-a|,只需-b∈{y|y=g(x),x∈[0,1]};故讨论g(x)=x|x-a|的值域即可.
解答:
解:(1)由题意得,x|x-1|-
=0;
①当x≥1时,x(x-1)=
;
解得x=
;
②当x<1时,x(1-x)=
;
解得x=
;
故函数f(x)的零点为
,
;
(2)函数f(x)在[0,1]上存在零点,即x|x-a|=-b在[0,1]上有解,
令g(x)=x|x-a|,只需-b∈{y|y=g(x),x∈[0,1]};
当a≤0时,g(x)=x|x-a|=x(x-a)在[0,1]递增,
所以g(x)∈[0,1-a],
即a-1≤b≤0;
当a≥1时,g(x)=x|x-a|=-x(x-a),对称轴x=
;
又当a≥2时,g(x)在[0,1]递增,所以g(x)∈[0,a-1],
即1-a≤b≤0;
当1<a<2时,g(x)在[0,
]递增,[
,1]递减,
所以g(x)∈[0,
],
即-
≤b≤0;
当0<a<1时,g(x)=x|x-a|=
;
易知,g(x)在[0,
]递增,[
,a]递减,[a,1]递减,
所以f(x)min=0,f(x)max={f(a),f(1)}={
,1-a},
当0<a≤2(
-1),f(x)max=f(1)=1-a,
所以g(x)∈[0,1-a],即a-1≤b≤0;
当2(
-1)<a<1,
f(x)max=f(a)=
,所以g(x)∈[0,
],
即-
≤b≤0;
综上所述:当a≤2(
-1)时,a-1≤b≤0;
当2(
-1)<a<2,-
≤b≤0;
当a≥2时,1-a≤b≤0.
| 1 |
| 4 |
①当x≥1时,x(x-1)=
| 1 |
| 4 |
解得x=
1+
| ||
| 2 |
②当x<1时,x(1-x)=
| 1 |
| 4 |
解得x=
| 1 |
| 2 |
故函数f(x)的零点为
1+
| ||
| 2 |
| 1 |
| 2 |
(2)函数f(x)在[0,1]上存在零点,即x|x-a|=-b在[0,1]上有解,
令g(x)=x|x-a|,只需-b∈{y|y=g(x),x∈[0,1]};
当a≤0时,g(x)=x|x-a|=x(x-a)在[0,1]递增,
所以g(x)∈[0,1-a],
即a-1≤b≤0;
当a≥1时,g(x)=x|x-a|=-x(x-a),对称轴x=
| a |
| 2 |
又当a≥2时,g(x)在[0,1]递增,所以g(x)∈[0,a-1],
即1-a≤b≤0;
当1<a<2时,g(x)在[0,
| a |
| 2 |
| a |
| 2 |
所以g(x)∈[0,
| a2 |
| 4 |
即-
| a2 |
| 4 |
当0<a<1时,g(x)=x|x-a|=
|
易知,g(x)在[0,
| a |
| 2 |
| a |
| 2 |
所以f(x)min=0,f(x)max={f(a),f(1)}={
| a2 |
| 4 |
当0<a≤2(
| 2 |
所以g(x)∈[0,1-a],即a-1≤b≤0;
当2(
| 2 |
f(x)max=f(a)=
| a2 |
| 4 |
| a2 |
| 4 |
即-
| a2 |
| 4 |
综上所述:当a≤2(
| 2 |
当2(
| 2 |
| a2 |
| 4 |
当a≥2时,1-a≤b≤0.
点评:本题考查了绝对值函数的应用,特别考查了分类讨论的数学思想应用,注意分类的标准,属于难题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
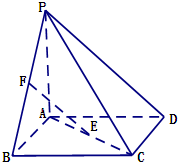 如图,四棱P-ABCD的底面ABCD为正方形,PA⊥底面ABCD,E、F分别是AC、PB的中点.
如图,四棱P-ABCD的底面ABCD为正方形,PA⊥底面ABCD,E、F分别是AC、PB的中点.