题目内容
4.已知平面上两点M(-5,0)和N(5,0),若直线上存在点P使|PM|-|PN|=6,则称该直线为“单曲型直线”,下列直线中:①y=x+1 ②y=2 ③y=$\frac{4}{3}$x ④y=2x+1
是“单曲型直线”的是①②.
分析 由已知点P在以M、N为焦点的双曲线的右支上,即$\frac{{x}^{2}}{9}-\frac{{y}^{2}}{16}=1$,(x>0).分别与①②③④中的直线联立方程组,根据方程组的解的性质判断该直线是否为“单曲型直线”.
解答 解:∵|PM|-|PN|=6∴点P在以M、N为焦点的双曲线的右支上,即$\frac{{x}^{2}}{9}-\frac{{y}^{2}}{16}=1$,(x>0).
对于①,联立$\left\{\begin{array}{l}{\frac{{x}^{2}}{9}-\frac{{y}^{2}}{16}=1}\\{y=x+1}\end{array}\right.$,消y得7x2-18x-153=0,
∵△=(-18)2-4×7×(-153)>0,∴y=x+1是“单曲型直线”.
对于②,联立$\left\{\begin{array}{l}{\frac{{x}^{2}}{9}-\frac{{y}^{2}}{16}=1}\\{y=2}\end{array}\right.$,消y得x2=$\frac{15}{4}$,∴y=2是“单曲型直线”.
对于③,联立$\left\{\begin{array}{l}{\frac{{x}^{2}}{9}-\frac{{y}^{2}}{16}=1}\\{y=\frac{x}{4}}\end{array}\right.$,整理得144=0,不成立.∴$y=\frac{4}{3}x$不是“单曲型直线”.
对于④,联立$\left\{\begin{array}{l}{\frac{{x}^{2}}{9}-\frac{{y}^{2}}{16}=1}\\{y=2x+1}\end{array}\right.$,消y得20x2+36x+153=0,
∵△=362-4×20×153<0∴y=2x+1不是“单曲型直线”.
故符合题意的有①②.
故答案为:①②.
点评 本题考查“单曲型直线”的判断,是中档题,解题时要认真审题,注意双曲线定义的合理运用.

 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
| A. | 对任意x∈R,都有x 2<ln2 | B. | 不存在x∈R,都有x 2<ln2 | ||
| C. | 存在x∈R,使得x 2≥ln2 | D. | 存在x∈R,使得x 2<ln2 |
| A. | l∥α | B. | l⊥α | ||
| C. | l?α | D. | l与α相交但不垂直 |
 石嘴山市在每年的春节后,市政府都会发动公务员参与到植树活动中去.林管部门在植树前,为保证树苗的质量,都会在植树前对树苗进行检测.现从甲乙两种树苗中各抽测了10株树苗的高度,量出的高度如下(单位:厘米)
石嘴山市在每年的春节后,市政府都会发动公务员参与到植树活动中去.林管部门在植树前,为保证树苗的质量,都会在植树前对树苗进行检测.现从甲乙两种树苗中各抽测了10株树苗的高度,量出的高度如下(单位:厘米)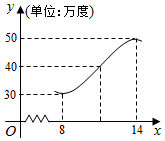 如图,某地夏天从8~14时用电量变化曲线近似满足函数y=Asin(ωx+φ)+b(ω>0,0<φ<π).
如图,某地夏天从8~14时用电量变化曲线近似满足函数y=Asin(ωx+φ)+b(ω>0,0<φ<π).