题目内容
函数f(x)=log2x-
的零点所在区间为 .
| 1 |
| x |
考点:二分法求方程的近似解
专题:计算题,函数的性质及应用
分析:连续函数f(x)=log2x-
在(0,+∞)上单调递增且f(1)=-1<0,f(1)=
>0,根据函数的零点的判定定理可求.
| 1 |
| x |
| 1 |
| 2 |
解答:
解:∵f(x)=log2x-
在定义域(0,+∞)上单调递增,
∴f(1)=-1<0,f(2)=
>0,
∴根据根的存在性定理得f(x)=log2x-
的零点所在的一个区间是(1,2),
故答案为:(1,2).
| 1 |
| x |
∴f(1)=-1<0,f(2)=
| 1 |
| 2 |
∴根据根的存在性定理得f(x)=log2x-
| 1 |
| x |
故答案为:(1,2).
点评:本题主要考查了函数零点定义及判定的应用,属于基础试题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
按照如图的程序框图执行,则输出的A值为( )


| A、255 | B、257 |
| C、511 | D、513 |
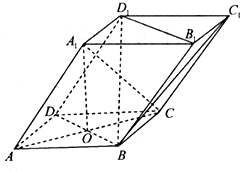 如图,四棱柱ABCD-A1B1C1D1的底面ABCD是菱形,AC,BD交于点O,A1O⊥平面ABCD,A1A=BD=2,AC=2
如图,四棱柱ABCD-A1B1C1D1的底面ABCD是菱形,AC,BD交于点O,A1O⊥平面ABCD,A1A=BD=2,AC=2