题目内容
P为△ABC所在平面外一点，O为P在平面ABC上的射影．（1）若PA=PB=PC，则O点是△ABC的 心；（2）若PA⊥BC，PB⊥AC，则点O是△ABC的 心；（3）若PA，PB，PC两两互相垂直，则O点是△ABC的 心．
考点：三角形五心
专题：证明题,空间位置关系与距离
分析：根据题意画出图形，然后一一判定即可．
解答：
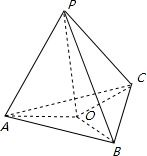解：（1）设点P作平面ABC的射影O，由题意：PA=PB=PC，因为PO⊥底面ABC，
所以△PAO≌△POB≌△POC
即：OA=OB=OC
所以O为三角形的外心．
（2）若PA⊥BC，PB⊥AC，因为PO⊥底面ABC，所以AO⊥BC，同理BO⊥AC，可得O是△ABC的垂心；
（3）若PA，PB，PC两两互相垂直，容易推出AO⊥BC，同理BO⊥AC，可得O是△ABC的垂心．
故答案为：外，垂，垂．
解：（1）设点P作平面ABC的射影O，由题意：PA=PB=PC，因为PO⊥底面ABC，所以△PAO≌△POB≌△POC
即：OA=OB=OC
所以O为三角形的外心．
（2）若PA⊥BC，PB⊥AC，因为PO⊥底面ABC，所以AO⊥BC，同理BO⊥AC，可得O是△ABC的垂心；
（3）若PA，PB，PC两两互相垂直，容易推出AO⊥BC，同理BO⊥AC，可得O是△ABC的垂心．
故答案为：外，垂，垂．
点评：本题考查棱锥的结构特征，三角形五心的定义，考查逻辑思维能力，是基础题．
练习册系列答案
相关题目
