题目内容
用定义证明：f（x）=x2-4x-3在（-∞，2]上为减函数．
考点：函数单调性的判断与证明
专题：证明题
分析：设x1＜x2≤2，通过作差法得到f（x1）＞f（x2），从而f（x）=x2-4x-3在（-∞，2]上为减函数．
解答：
证明：设x1＜x2≤2，
∴f（x1）-f（x2）=（x1-x2）（x1+x2-4），
∵x1-x2＜0，x1+x2-4＜0，
∴f（x1）＞f（x2），
∴f（x）=x2-4x-3在（-∞，2]上为减函数．
∴f（x1）-f（x2）=（x1-x2）（x1+x2-4），
∵x1-x2＜0，x1+x2-4＜0，
∴f（x1）＞f（x2），
∴f（x）=x2-4x-3在（-∞，2]上为减函数．
点评：本题考查了函数的单调性的证明，用定义证明时，通常采用作差法，本题是一道基础题．
练习册系列答案
云南师大附小一线名师提优作业系列答案
相关题目
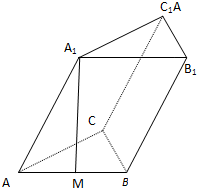已知斜三棱柱ABC-A1B1C1的底面是正三角形，侧面ABB1A1是菱形，且∠A1AB=60°，M是AB的中点，A1M⊥AC