题目内容
19．△ABC中，a，b，c分别是角A，B，C所对的边，2bsinB=（2a+c）sinA+（2c+a）sinC（1）求∠B的大小；
（2）若a=4，A=45°，求c的值．
分析 （1）由正弦定理化简已知可得b2=a2+c2+ac，进而利用余弦定理得cosB=-$\frac{1}{2}$，结合范围0°＜B＜180°，可求B的值．
（2）利用三角形内角和定理可求C，由正弦定理即可计算得解c的值．
解答 解：（1）由正弦定理$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}$，又由已知2bsinB=（2a+c）sinA+（2c+a）sinC，
可得：b2=a2+c2+ac，①…（1分）
由余弦定理得：cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$，②
①代入得②，可得：cosB=-$\frac{1}{2}$，…（2分）
又0°＜B＜180°，…（3分）
所以有∠B=120°，…（4分）
（2）由（1）得B=120°，又A=45°，
∴C=15°．…（5分）
由正弦定理得$\frac{a}{sinA}=\frac{c}{sinC}$，即$\frac{4}{sin45°}=\frac{c}{sin15°}$，…（6分）
∴c=4×$\frac{\sqrt{6}-\sqrt{2}}{4}$×$\frac{2}{\sqrt{2}}$=2$\sqrt{3}$-2．…（8分）
点评 本题主要考查了正弦定理，余弦定理，三角形内角和定理在解三角形中的综合应用，考查了计算能力和转化思想，属于基础题．
练习册系列答案
相关题目
如图，点A的坐标为（1，0），函数y=ax2过点C（2，4），若在矩形ABCD内随机取一点，则此点取自阴影部分的概率等于$\frac{5}{12}$．
10．如图是一个算法的流程图，若输入x的值为4，则输出y的值 是（ ）
| A． | -3 | B． | -2 | C． | -1 | D． | 0 |
7．
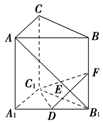直三棱柱ABC-A1B1C1中，侧棱长为2，AC=BC=1，∠ACB=90°，D是A1B1的中点，F是BB1上的动点，AB1，DF交于点E，要使AB1⊥平面C1DF，则线段B1F的长为（ ）
直三棱柱ABC-A1B1C1中，侧棱长为2，AC=BC=1，∠ACB=90°，D是A1B1的中点，F是BB1上的动点，AB1，DF交于点E，要使AB1⊥平面C1DF，则线段B1F的长为（ ）| A． | $\frac{1}{2}$ | B． | 1 | C． | $\frac{3}{2}$ | D． | 2 |
4．已知m，n是满足m+n=1，且使$\frac{1}{m}+\frac{9}{n}$取得最小值的正实数，若函数y=xa过点 P（m，$\frac{2}{3}$n），则α的值为（ ）
| A． | 3 | B． | 2 | C． | $\frac{1}{2}$ | D． | -1 |