题目内容
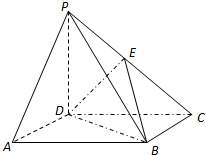 如图所示,PD⊥底面ABCD,四边形ABCD是正方形,PD=DC,E是PC的中点.
如图所示,PD⊥底面ABCD,四边形ABCD是正方形,PD=DC,E是PC的中点.(1)证明:PA∥平面BDE;
(2)求二面角B-DE-C的平面角的余弦值.
考点:二面角的平面角及求法,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(1)连结AC、BD,交于O,连结OE,由已知得OE∥AP,由此能证明PA∥平面BDE.
(2)以D为原点,DA为x轴,DC为y轴,DP为z轴,建立空间直角坐标系,利用向量法能求出二面角B-DE-C的平面角的余弦值.
(2)以D为原点,DA为x轴,DC为y轴,DP为z轴,建立空间直角坐标系,利用向量法能求出二面角B-DE-C的平面角的余弦值.
解答:
(1)证明:连结AC、BD,交于O,连结OE,
∵四边形ABCD是正方形,∴O是AC中点,
∵E是PC的中点,∴OE∥AP,
∵AP不包含于平面BDE,OE?平面BDE,
∴PA∥平面BDE.
(2)解:以D为原点,DA为x轴,DC为y轴,DP为z轴,
建立空间直角坐标系,
∵四边形ABCD是正方形,PD=DC,设PD=DC=2,
∴B(2,2,0),D(0,0,0),C(0,2,0),
P(0,0,2),E(0,1,1),
=(0,1,1),
=(2,2,0),
则
,
取x=1,得
=(1,-1,1),
又平面DEC的法向量
=(1,0,0),
设二面角B-DE-C的平面角为θ,
则cosθ=cos<
,
>=
=
.
∴二面角B-DE-C的平面角的余弦值为
.

∵四边形ABCD是正方形,∴O是AC中点,
∵E是PC的中点,∴OE∥AP,
∵AP不包含于平面BDE,OE?平面BDE,
∴PA∥平面BDE.
(2)解:以D为原点,DA为x轴,DC为y轴,DP为z轴,
建立空间直角坐标系,
∵四边形ABCD是正方形,PD=DC,设PD=DC=2,
∴B(2,2,0),D(0,0,0),C(0,2,0),
P(0,0,2),E(0,1,1),
| DE |
| DB |
则
|
取x=1,得
| n |
又平面DEC的法向量
| m |
设二面角B-DE-C的平面角为θ,
则cosθ=cos<
| n |
| m |
| 1 | ||
|
| ||
| 3 |
∴二面角B-DE-C的平面角的余弦值为
| ||
| 3 |
点评:本题考查直线与平面平行的证明,考查二面角的余弦值的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
 某企业为更好地了解设备改造前后与生产合格品的关系,随机抽取了100件产品进行分析,但由于工作人员不小心,丢失了部分数据:设备改造效果分析列联表
某企业为更好地了解设备改造前后与生产合格品的关系,随机抽取了100件产品进行分析,但由于工作人员不小心,丢失了部分数据:设备改造效果分析列联表 如图,二面角α-l-β的大小是45°,线段AB?α.B∈l,AB与l所成的角为30°.则AB与平面β所成的角的正弦值是
如图,二面角α-l-β的大小是45°,线段AB?α.B∈l,AB与l所成的角为30°.则AB与平面β所成的角的正弦值是